Giải bài tập phát triển năng lực toán lớp 9 bài 6: Tính chất của hai tiếp tuyến cắt nhau

1. Tìm x trong mỗi trường hợp ở hình 6.6, biết rằng AB và AD là tiếp tuyến của đường trò tâm C (B, D là tiếp điểm).

2. GPS (viết tắt của Global Positioning System) là hệ thống định vị toàn cầu, hệ thống xác định vị trí trên mặt đất dự vào vị tríc của các vệ tinh nhân tạo do bộ quốc phòng Hoa Kỳ thiết kế, xây dựng, vận hành, và quản lí. Vệ tinh GPS không thể truyền tải trực tiếp tín hiệu đến Trái Đất mà phải qua các trạm thu đặt tại điểm A và C. Biết rằng một vệ tinh B luôn quay xung quanh Trái Đất với khoảng cách xấp xỉ 17700 km, bán kính của Trái Đất xấp xỉ 6400 km.

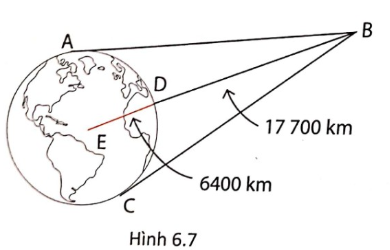
a, Tính quãng đường truyền tín hiệu từ vệ tinh ở vị trí B đến các trạm thu tại A và C.

b, Tìm số đo các góc ABD và ABC.

3. Cho đoạn thẳng AB. Tren cùng một nửa mặt phẳng bờ AB, vẽ nửa đường tròn (O) đường kính AB và các tiếp tuyến Ax, By. Trên nửa đường tròn tâm O lấy điểm M, qua M vẽ tiếp tuyến với đường tròn, cắt Ax, By lần lượt tại C và D (hình 6.8).

a, Chứng minh rằng tứ giác ACDB là hình thang vuông.

b, Chứng minh rằng các tam giác ACM và BDM cân.

c, Chứng minh rằng AB là tiếp tuyến cua đường tròn đường kính CD.

d, Gọi N là giao điểm của AD và BC. Chứng minh rằng MN vuông góc với AB.

e, Chứng minh rằng khi M di chuyển trên nửa đường tròn thì tích AC.BD không đổi.

f, Tìm vị trí của M trên nửa đường tròn để diện tích tứ giác ACDB nhỏ nhất. Tính diện tích nhỏ nhất của tứ giác ACDB theo AB.

4. Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ dường tròn tâm O tiếp xúc với AB, AC tại H và K. Một tiếp tuyến với đường tròn (O) tại E cắt các cạnh AB, Ac tại M và N. 

a, Chứng minh rằng $\widehat{MON}=\frac{1}{2}\widehat{HOK}$

b, Giả sử $\widehat{B}=50^{0}$, tính góc MON.

c, Chứng minh rằng tam giác BMO và CON đồng dạng với nhau.

d, Chứng minh rằng tích BM.CN không đổi khi tiếp tuyến với đường tròn (O) thay đổi.

e, Tìm vị trí tiếp tuyến với đường tròn (O) tại E để tổng BM + CN là nhỏ nhất.

5. Cho đường tròn (O; r) nội tiếp tam giác ABC. Các tiếp tuyến với đường tròn (O) song song với các cạnh của tam giác ABC chia tam giác ABC thành ba tam giác nhỏ. Gọi r₁, r₂, r₃ lần lượt là bán kính của các đường tròn nội tiếp và P₁, P₂, P₃ tương ứng là chu vi cảu ba tam giác nhỏ đó. Gọi P là chu vi của tam giác ABC. Chứng minh rằng:

a, P₁ + P₂ + P₃  = P

b, r₁ + r₂ + r₃ = r

6. Cho tam giác ABC. Gọi a, b, c lần lượt là các cạnh; h_a, h_b, h_c là các đường cao tương ứng; R_a, R_b, R_c lần lượt là bán kính các đường tròn bàng tiếp tương ứng trong các góc A, B, C; r là bán kính của đường tròn nội tiếp; p là nửa chu vi tam giác; S là diện tích tam giác. Chứng minh rằng:

a, S = R_a(p - a) = R_b(p - b) = R_c(p - c)

b, $\frac{1}{r}=\frac{1}{R_{a}}+\frac{1}{R_{b}}+\frac{1}{R_{c}}$;

c, $\frac{1}{R_{a}}=\frac{1}{h_{c}}+\frac{1}{h_{b}}-\frac{1}{h_{a}}$;