Giải bài tập phát triển năng lực toán lớp 9 bài 1: Một số hệ thức về cạnh và đường cao trong tam giác vuông

1. Cho tam giác ABC vuông tại A, đường cao AH, AB = 6cm, AC = 8cm (hình 1.6).

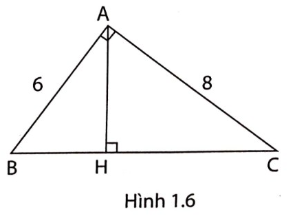
a, Em hãy điền vào chỗ chấm để hoàn thành lời giải tìm BH, AH.

Xét tam giác ABC vuông tại A, đường cao AH.

Ta có:

* BC$^{2}$ = ............................ (định lí Py-ta-go)

= ........................ (vì AB = 6cm; AC = 8cm)

=> BC = .............

* AH.BC =  ......................... (hệ thức giữa cạnh và đường cao trong tam giác vuông)

=> AH.BC = ...................... (Vì ................................)

=> AH = ........................

* ........................... = BH.BC (hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền)

=> ......................... = BH.(.........) (vì ...............................)

=> BH = .................

b, Em hãy tìm thêm các cách khác để tính BH, AH.

2. Cho tam giác ABC vuông tại A, đường cao AH. Mỗi hình vẽ sau cho biết độ dài của hai trong 6 đoạn AB, AC, BC, HA, HB, HC (hình 1.7). Em hãy tìm độ dài các đoạn thẳng còn lại trong từng hình. Dựa vào cách trình bày của bài 1a, hình trình bày lời giải của em.

3. a, Cho hình 1.8, chứng minh rằng:

$b^{2}-c^{2}=b'^{2}-c'^{2}$;  $\left ( \frac{b}{c} \right )^{2}=\frac{b'}{c'}$.

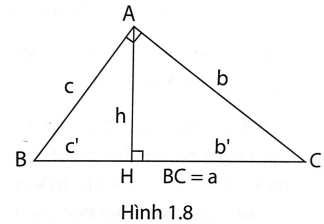
b, Vận dụng kết quả trong câu a giải các bài toán sau:

i. Cho tam giác ABC có $\widehat{A}=90^{0}$, đường cao AH, $\frac{HB}{HC}=\frac{1}{4}$, BC = 25. Tính AB, AC, HB, HC, AH.

ii. Cho tam giác ABC có $\widehat{A}=90^{0}$, đường cao AH, $\frac{HB}{HC}=\frac{9}{16}$, AH = 24. Tính BC, AB, AC, HB, HC.

iii. Cho tam giác ABC có $\widehat{A}=90^{0}$, đường cao AH, $\frac{AB}{AC}=\frac{3}{4}$, BC = 125. Tính AB, AC, HB, HC, AH.

iv. Cho tam giác ABC có $\widehat{A}=90^{0}$, đường cao AH, $\frac{AB}{AC}=\frac{5}{6}$, AH = 30. Tính BC, AB, AC, HB, HC.

4. Hình 1.9 là hình ảnh của một chiếc thước thợ (thước của thợ mộc dùng để đo góc vuông).

Làm thế nào để "đo" chiều cao của một cái cây bằng một chiếc thước thợ?

Em hãy đọc nội dung sau và cùng làm với Nam nhé.

Bạn Nam đã chọn được vị trí mà tại đó bạn ngắm dọc theo một cạnh của thước thì thẳng tới gốc cây, còn ngắm dọc theo cạnh kia thì thẳng tới ngọn cây (hình 1.10).

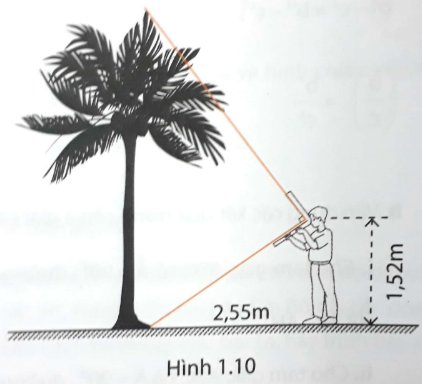
Bạn đo được khoảng cách từ vị trí đứng đến gốc cây là 2,55m, khoảng cách từ mắt bạn đến mặt đất là 1,52m.

a, Coi các vị trí: gốc cây, ngọn cây, mắt nhìn, vị trí đứng là các điểm. Em hãy đặt tên cho các điểm đó và chuyển nội dung bài toán đo chiều cao của cây thành bài tập hình học.

b, Ta thấy vị trí mắt nhìn với gốc cây và đỉnh ngọn cây tạo thành một tam giác vuông. Em hãy thiết lập công thức tính chiều cao của cây theo các yếu tố đã biết.

c, Hãy sử dụng máy tính bỏ túi để tính chiều cao của cây theo đơn vị mét (làm tròn đến chữ số thập phân thứ hai).

5. Cho tam giác ABC có $\widehat{A}=90^{0}$, đường cao AH. Kẻ HM $\perp $ AB tại M, HN $\perp $ AC tại N. Chứng minh:

a, AM.AB = AN.AC = HB.HC

b, AM.AB + AN.AC = 2.MN$^{2}$

c, $\frac{AB^{3}}{AC^{3}}=\frac{BM}{CN}$

d, AM.BM + AN.CN = AH$^{2}$

e, HM.AB + HN.AC = AB.AC

f, $\frac{1}{HM^{2}}=\frac{1}{AB^{2}}+\frac{1}{AC^{2}}+\frac{1}{BH^{2}}$

g, MN$^{3}$ = BC.BM.CN