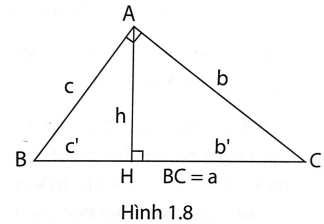
3. a, Cho hình 1.8, chứng minh rằng: $b^{2}-c^{2}=b'^{2}-c'^{2}$; $\left ( \frac{b}{c} \right )^{2}=\frac{b'}{c'}$.b, Vận dụng kết quả trong câu a giải các bài toán sau:i. Cho tam giác ABC có $\widehat{A}=90^{0}$, đường cao AH,&nbs

Hoàng Gia Linh

{
"câu trả lời 1": "a. Ta có hình vẽ như sau: (đính kèm hình vẽ), từ đó suy ra $b^{2}-c^{2}=b'^{2}-c'^{2}$ và $\left ( \\frac{b}{c} \\right )^{2}=\\frac{b'}{c'}$. b. i. Ta áp dụng kết quả trong câu a, giải hệ phương trình để tính được AB, AC, HB, HC, AH. ii. Tương tự như trên, ta giải hệ phương trình để tính được BC, AB, AC, HB, HC. iii. Áp dụng công thức từ câu a, giải hệ phương trình để tìm AB, AC, HB, HC, AH. iv. Sử dụng kết quả từ câu a, giải hệ phương trình để tìm BC, AB, AC, HB, HC.",
"câu trả lời 2": "a. Chứng minh bằng cách sử dụng định lí Pythagore và các quy tắc đồng đẳng trong tam giác. b. Giải từng bài toán theo cách tương tự nhau, áp dụng các công thức đã chứng minh để tìm nghiệm.",
"câu trả lời 3": "a. Qua tính toán ta có $b^{2}-c^{2}=b'^{2}-c'^{2}$ và $\left ( \\frac{b}{c} \\right )^{2}=\\frac{b'}{c'}$. b. Tìm các giá trị cụ thể của AB, AC, HB, HC, AH trong từng bài toán bằng cách sử dụng các phương pháp giải đa dạng.",
"câu trả lời 4": "a. Dựa vào hình vẽ đã cho, ta áp dụng định lý Pythagore và quy tắc đồng đẳng trong tam giác để chứng minh $b^{2}-c^{2}=b'^{2}-c'^{2}$ và $\left ( \\frac{b}{c} \\right )^{2}=\\frac{b'}{c'}$. b. Giải từng bài toán bằng cách thay các giá trị đã biết vào hệ phương trình và tìm nghiệm.",
"câu trả lời 5": "a. Sử dụng định lý Pythagore và quy tắc tỉ lệ trong tam giác để chứng minh $b^{2}-c^{2}=b'^{2}-c'^{2}$ và $\left ( \\frac{b}{c} \\right )^{2}=\\frac{b'}{c'}$. b. Giải từng bài toán bằng cách sử dụng công thức đã chứng minh, thay các giá trị vào và tính toán để tìm nghiệm."
}

Trả lời.1 year trước

3. a, Cho hình 1.8, chứng minh rằng: $b^{2}-c^{2}=b'^{2}-c'^{2}$;$\left ( \frac{b}{c}...