1. Cho tam giác ABC vuông tại A, đường cao AH, AB = 6cm, AC = 8cm (hình 1.6).a, Em hãy điền vào chỗ...
1. Cho tam giác ABC vuông tại A, đường cao AH, AB = 6cm, AC = 8cm (hình 1.6).
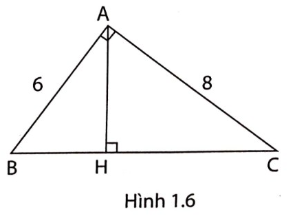
a, Em hãy điền vào chỗ chấm để hoàn thành lời giải tìm BH, AH.
Xét tam giác ABC vuông tại A, đường cao AH.
Ta có:
* BC$^{2}$ = ............................ (định lí Py-ta-go)
= ........................ (vì AB = 6cm; AC = 8cm)
=> BC = .............
* AH.BC = ......................... (hệ thức giữa cạnh và đường cao trong tam giác vuông)
=> AH.BC = ...................... (Vì ................................)
=> AH = ........................
* ........................... = BH.BC (hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền)
=> ......................... = BH.(.........) (vì ...............................)
=> BH = .................
b, Em hãy tìm thêm các cách khác để tính BH, AH.
- 2. Cho tam giác ABC vuông tại A, đường cao AH. Mỗi hình vẽ sau cho biết độ dài của hai trong 6 đoạn...
- 3. a, Cho hình 1.8, chứng minh rằng: $b^{2}-c^{2}=b'^{2}-c'^{2}$;$\left ( \frac{b}{c}...
- 4. Hình 1.9 là hình ảnh của một chiếc thước thợ (thước của thợ mộc dùng để đo góc vuông).Làm thế...
- 5. Cho tam giác ABC có$\widehat{A}=90^{0}$, đường cao AH. Kẻ HM $\perp $ AB tại M, HN $\perp...






Đặt x là chiều dài của BH, với AH là độ dài cố định, ta có: AH/x = x/AC => x^2 = AH.AC = 4.8.8 = 38.4 => x = √38.4 ≈ 6.2cm
Sử dụng công thức Pythagore trong tam giác AHB: BH^2 = AB^2 - AH^2 = 6^2 - 4.8^2 = 36 - 23.04 = 12.96 => BH = √12.96 ≈ 3.6cm
AH/BC = BH/AC (vì AH và BH cùng là chiều cao của tam giác) => AH/10 = BH/8 => BH = 10/8 * 4.8 = 6cm
AH.BC = AB.AC => AH.10 = 6.8 => AH = 4.8cm
BC^2 = AB^2 + AC^2 = 6^2 + 8^2 = 36 + 64 = 100 => BC = 10cm