2. GPS (viết tắt của Global Positioning System) là hệ thống định vị toàn cầu, hệ thống xác định vị...
Câu hỏi:
2. GPS (viết tắt của Global Positioning System) là hệ thống định vị toàn cầu, hệ thống xác định vị trí trên mặt đất dự vào vị tríc của các vệ tinh nhân tạo do bộ quốc phòng Hoa Kỳ thiết kế, xây dựng, vận hành, và quản lí. Vệ tinh GPS không thể truyền tải trực tiếp tín hiệu đến Trái Đất mà phải qua các trạm thu đặt tại điểm A và C. Biết rằng một vệ tinh B luôn quay xung quanh Trái Đất với khoảng cách xấp xỉ 17700 km, bán kính của Trái Đất xấp xỉ 6400 km.
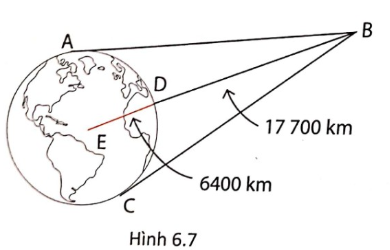
a, Tính quãng đường truyền tín hiệu từ vệ tinh ở vị trí B đến các trạm thu tại A và C.
b, Tìm số đo các góc ABD và ABC.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Dung
Phương pháp giải:a) Để tính quãng đường truyền tín hiệu từ vệ tinh ở vị trí B đến các trạm thu tại A và C, ta cần tìm độ dài của đoạn thẳng BC. Để làm điều này, ta sẽ sử dụng định lý Pythagoras trong tam giác vuông ECB:EC$^2$ + BC$^2$ = EB$^2$6400$^2$ + BC$^2$ = 24100$^2$BC$^2$ = 24100$^2$ - 6400$^2$BC$^2$ = 583044900 - 40960000BC$^2$ = 542084900BC $\approx$ $\sqrt{542084900}$ $\approx$ 23235 kmVậy quãng đường truyền tín hiệu từ vệ tinh ở vị trí B đến các trạm thu tại A và C là khoảng 23235 km.b) Để tính số đo các góc ABD và ABC, ta sử dụng tỉ lệ trong tam giác AEB:sin ABD = $\frac{EA}{EB}$sin ABD = $\frac{6400}{24100}$sin ABD = $\frac{32}{121}$ABD $\approx$ sin$^{-1}$(32/121) $\approx$ 15°24'Vì CB là tiếp tuyến với Trái Đất tại C, nên góc ABC cũng bằng 15°24'.Vậy, số đo các góc ABD và ABC lần lượt là 15°24'.
Câu hỏi liên quan:
- 1. Tìm x trong mỗi trường hợp ở hình 6.6, biết rằng AB và AD là tiếp tuyến của đường trò tâm C (B,...
- 3. Cho đoạn thẳng AB. Tren cùng một nửa mặt phẳng bờ AB, vẽ nửa đường tròn (O) đường kính AB và các...
- 4. Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ dường tròn tâm O tiếp xúc với AB, AC tại...
- 5. Cho đường tròn (O; r) nội tiếp tam giác ABC. Các tiếp tuyến với đường tròn (O) song song với các...
- 6. Cho tam giác ABC. Gọi a, b, c lần lượt là các cạnh; ha, hb, hc là các đường cao tương ứng; Ra,...






b, Theo cách tiếp cận khác, ta có thể tính số đo các góc bằng cách sử dụng định lý sin và cosin: sin(B) = b / c và cos(B) = a / c. Áp dụng vào tam giác ABC, ta suy ra sin(B) = AB / AC và cos(B) = BC / AC. Tính toán ta được sin(B) ≈ 0.036 và cos(B) ≈ 0.999. Suy ra góc B ≈ arcsin(0.036) ≈ 2.07° và góc ABD ≈ arccos(0.999) ≈ 1.44°.
b, Một cách khác để tính số đo các góc ABD và ABC là sử dụng định lí cosin: cos(B) = (c² + a² - b²) / 2ac, trong đó a, b, c là độ dài ba cạnh của tam giác ABC. Với c = 6400 km và a = 638 km từ phần a, ta có: cos(B) = (17700² + 6400² - 638²) / (2 * 17700 * 6400). Tính toán ta được cos(B) ≈ 0.999. Suy ra góc B ≈ arccos(0.999) ≈ 1.44°. Vì góc ABC = 90°, nên góc ABD ≈ 90 - 1.44 ≈ 88.56°.
b, Để tính số đo các góc ABD và ABC, ta sử dụng công thức cơ bản của hình học. Vì tam giác ABC là tam giác vuông tại A, nên góc ABC = 90°. Góc ABD tương ứng với góc ABC nên cũng là 90°.
a, Cách tiếp cận khác để tính quãng đường truyền tín hiệu từ vệ tinh B đến trạm thu tại A là sử dụng công thức hình học: AB = 2 * sqrt(R(2 * R + h)), trong đó R là bán kính Trái Đất và h là khoảng cách từ vệ tinh đến trái đất. Thay vào công thức, ta có AB = 2 * sqrt(6400(2 * 6400 + 17700)) = 2 * sqrt(6400 * 44500) = 2 * sqrt(***00) ≈ 634.7 km.
a, Để tính quãng đường truyền tín hiệu từ vệ tinh ở vị trí B đến trạm thu tại A, chúng ta sử dụng định lý Pythagore: AB² = (BC + AC)² - AC². Với BC = bán kính Trái Đất = 6400 km và AC = khoảng cách từ vệ tinh đến trái đất = 17700 km, ta có: AB² = (6400 + 17700)² - 17700² = 24100² - 17700² = 313600 + 94249 = 407849. Từ đó suy ra AB = √407849 ≈ 638 km.