5. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi E là điểm đối xứng với B qua H....
5. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi E là điểm đối xứng với B qua H. Đường tròn đường kính EC cắt AC tại K (hình 5.7).
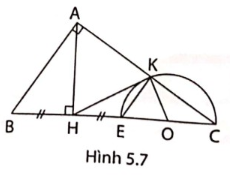
Chứng minh rằng:
a, Tứ giác AKEB là hình thang vuông.
b, Tam giác AHK cân,
c, HK là tiếp tuyến của đường tròn đường kính EC.
a, Gọi O là tâm đường tròn đường kính EC => OK = OC = OE (bán kính của đường tròn)
+ Xét tam giác EKC có:
- KO là trung tuyến ứng với cạnh EC (OE = OC)
- KO = $\frac{1}{2}$EC
=> Tam giác EKC vuông tại K (tính chất đường trung tuyến ứng với cạnh huyền của tam giác vuông)
=> EK $\perp $ KC hay EK $\perp $ AC
+ EK $\perp $ AC và BA $\perp $ AC => EK // BA
+ Tứ giác AKEB có EK // BA => AKEB là hình thang
+ Hình thang AKEB có $\widehat{BAK}=90^{0}$
=> AKEB là hình thang vuông
b, Trên AK lấy I là trung điểm của AK => HI là đường trung bình của hình thang vuông AKEB
=> HI $\perp $ AK
+ Xét tam giác AHI và KHI có:
- Chung cạnh HI
- AK = KI
- $\widehat{AIH}=\widehat{KIH}=90^{0}$
=> $\Delta $AHI = $\Delta $KHI (c.g.c)
=> AH = KH
+ Xét tam giác AHK có AH = KH
=> Tam giác AHK cân tại H
c, $\widehat{HAK}=\widehat{AKH}$ (Tam giác AHK cân tại H)
Tam giác OKE cân tại O (OK = OE) => $\widehat{KEC}=\widehat{EKO}$
+ $\widehat{HAK}+\widehat{KCE}= 90^{0}$ (vì $\widehat{AHC}=90^{0}$)
+ $\widehat{KCE}+\widehat{KEC}= 90^{0}$ (Tam giác EKC vuông tại K)
=> $\widehat{HAK}=\widehat{KEC}$
=> $\widehat{HKA}=\widehat{KEC}$ (= $\widehat{HAK}$)
=> $\widehat{HKA}=\widehat{EKO}$ (= $\widehat{KEC}$)
+ Ta có: $\widehat{HKA}+\widehat{EKH}=\widehat{EKA}=90^{0}$ (Vì $\widehat{EKA}=90^{0}$)
=> $\widehat{EKO}+\widehat{EKH}=90^{0}$ (Vì $\widehat{HKA}=\widehat{EKO}$)
<=> $\widehat{HKO}=90^{0}$ => OK $\perp $ HK
+ Xét đường tròn tâm O và đường thẳng HK có:
- K là điểm chung duy nhất
- Bán kính OK $\perp $ HK
=> HK là tiếp tuyến của đường tròn O tại K
- 1. Tìm bán kính của đường tròn (C) trong những trường hợp ở hình 5.4:
- 2. a, Đánh dấu "X" vào bên cạnh chỗ chấm tương ứng với khẳng định đúng dưới đây:Nếu dường thẳng d...
- 3. Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm B bán kính BA và đường tròn tâm C bán kính CA...
- 4. Cho tam giác ABC cân tại A. Các đường cao AD, BE của tam giác cắt nhau tại H. Gọi O là trung...






c. Gọi M là giao điểm của HK và AC. Ta có góc HME = góc KCE (cùng chiều quay với AC) và góc HEM = góc CKE (cùng chiều quay với AC). Do đó, tam giác HME và tam giác KCE đồng dạng. Từ đó, ta suy ra HK là tiếp tuyến của đường tròn đường kính EC.
b. Ta có góc HKA = 90 độ (do HK là tiếp tuyến của đường tròn đường kính EC và góc ở ngoài của tam giác bằng tổng hai góc ở trong). Và góc HAK = góc KCE (cùng chiều quay với AC). Vậy tam giác AHK cân.
a. Ta có AE // BC, do E là điểm đối xứng của B qua H. Vậy ta có góc AKE = góc ABC (cùng chiều quay với AC). Và ta có góc KEA = góc KCA (cùng chiều quay với AC). Như vậy, tứ giác AKEB là hình thang vuông.