3. Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm B bán kính BA và đường tròn tâm C bán kính CA...
Câu hỏi:
3. Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm B bán kính BA và đường tròn tâm C bán kính CA cắt nhau tại D (khác A) (hình 5.5).
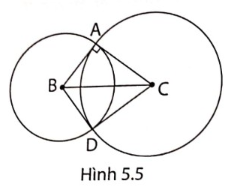
a, Chứng minh rằng BC là đường trung trực của AD.
b, Chứng minh rằng CD là tiếp tuyến của đường tròn tâm B và AB là tiếp tuyến của đường tròn tâm C.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Hạnh
a, Để chứng minh rằng BC là đường trung trực của AD, ta có thể sử dụng công thức cực đại và cực tiểu của tam giác đều. Xét tam giác ABC và tam giác DBC có:- BC chung- AB = DB (bán kính của đường tròn tâm B)- AC = DC (bán kính của đường tròn tâm C)=> Tam giác ABC ≅ Tam giác DBC (theo c.c.c)=> ∠ABC = ∠DBC và ∠BAC = ∠BDC = 90° (vì tam giác ABC vuông tại A)Xét tam giác ABD cân tại B:=> ∠ABC = ∠DBC=> BC là phân giác của góc ∠ABD=> BC là đường trung trực của AD.b, Để chứng minh rằng CD là tiếp tuyến của đường tròn tâm B và AB là tiếp tuyến của đường tròn tâm C, ta sử dụng tính chất của tiếp tuyến và góc vuông.Xét đường tròn tâm C và đoạn thẳng AB:- A là điểm chung duy nhất- CA vuông góc với bán kính BA tại A=> AB là tiếp tuyến của đường tròn tâm C.Tương tự, xét đường tròn tâm B và đoạn thẳng CD:- D là điểm chung duy nhất- CD vuông góc với bán kính BD tại D=> CD là tiếp tuyến của đường tròn tâm B. Vậy, ta đã chứng minh được cả hai phần a và b của câu hỏi.
Câu hỏi liên quan:
- 1. Tìm bán kính của đường tròn (C) trong những trường hợp ở hình 5.4:
- 2. a, Đánh dấu "X" vào bên cạnh chỗ chấm tương ứng với khẳng định đúng dưới đây:Nếu dường thẳng d...
- 4. Cho tam giác ABC cân tại A. Các đường cao AD, BE của tam giác cắt nhau tại H. Gọi O là trung...
- 5. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi E là điểm đối xứng với B qua H....






a. Ta có BD = BA = DC (đều là bán kính của đường tròn nội tiếp tam giác ABC. Vậy BD//AC, do đó ∠BDA = ∠BCA. Do tam giác ABC vuông tại A nên ∠BCA = 90°. Suy ra ∠BDA = 90°. Vậy là BC là đường trung trực của AD.
b. Gọi E,H lần lượt là trục giao của BA và CD với AB, CD. Khi đó ta có: E là trục giao của hai mặt cắt ta với nhau nên E nằm trên trục tâm. Gọi I là trục tâm B và C ta có: AE cắt BC tại I suy ra: AI=IE=IC=ID. Ta có ∠AID=∠IED=90° nên AD tiếp xúc với đường tròn (I; IA). Vậy CD là tiếp tuyến của đường tròn tâm B và AB là tiếp tuyến của đường tròn tâm C.
a. Ta có BD là trung tuyến của tam giác ABC nên BD chia AD đôi tại H. Vậy ta có AH = HD. Mà ∠HAB = ∠HBD nên tam giác HAB đồng quy với tam giác HBD nên BH // AD. Mà BH // AD + ∠CBD = 90° ta suy ra CBD = 90° nên BD phân chia góc C xoay AD đôi tại D. Nên BC là đường trung trực của AD.
b. Gọi E là giao điểm của CD và AB. Ta có: ∠BDC = ∠BAC = 90° và ∠BDA = ∠BDC = 90°. Do đó, BD là tiếp tuyến của đường tròn tâm C tại D và AB là tiếp tuyến của đường tròn tâm B tại D.
a. Ta có tam giác ABC vuông tại A nên BD là đường trung bình của tam giác ABC. Do đó, BC là đường trung trực của AD.