4. Cho tam giác ABC cân tại A. Các đường cao AD, BE của tam giác cắt nhau tại H. Gọi O là trung...
Câu hỏi:
4. Cho tam giác ABC cân tại A. Các đường cao AD, BE của tam giác cắt nhau tại H. Gọi O là trung điểm của AH (hình 5.6).
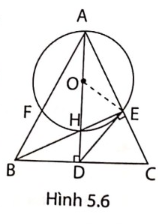
a, Chứng minh rằng điểm E nằm trên đường tròn tâm O đường kính AH.
b, Gọi F là giao điểm của đường tròn O với cạnh AB. Chứng minh ba điểm C, H, F thẳng hàng.
c, Chứng minh rằng DE là tiếp tuyến của đường tròn O.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Ánh
a, Điểm E nằm trên đường tròn tâm O đường kính AH bằng cách chứng minh rằng OE là bán kính của đường tròn tâm O đường kính AH.b, Ba điểm C, H, F thẳng hàng được chứng minh bằng cách chứng minh rằng HF vuông góc với AB, sau đó chứng minh 3 điểm C, H, F đều thuộc cùng một đường thẳng.c, Chứng minh rằng DE là tiếp tuyến của đường tròn O bằng cách chứng minh rằng DE vuông góc với OE và DE chỉ cắt đường tròn O tại một điểm duy nhất.
Câu hỏi liên quan:
- 1. Tìm bán kính của đường tròn (C) trong những trường hợp ở hình 5.4:
- 2. a, Đánh dấu "X" vào bên cạnh chỗ chấm tương ứng với khẳng định đúng dưới đây:Nếu dường thẳng d...
- 3. Cho tam giác ABC vuông tại A. Vẽ đường tròn tâm B bán kính BA và đường tròn tâm C bán kính CA...
- 5. Cho tam giác ABC vuông tại A (AB < AC), đường cao AH. Gọi E là điểm đối xứng với B qua H....






c. Ta có góc OAH = 60 độ và góc EAD = 90 độ (do DE là đường cao của tam giác ADE). Như vậy, góc OAE = 180 - 60 - 90 = 30 độ. Do tam giác OAE là tam giác đều nên góc AEO = góc AOE = 75 độ. Mà góc ADE = góc AOE nên DE là tiếp tuyến của đường tròn O.
b. Ta có O là trung điểm của AH nên OA = OH. Như vậy, tam giác OAH là tam giác đều nên góc OAH = góc OHA = 60 độ. Do tam giác ABC là tam giác cân tại A nên góc ABC = góc ACB. Mà góc OAH = góc ABC nên ba điểm C, H, F thẳng hàng.
a. Ta có O là trung điểm của AH nên OA = OH. Như vậy, tam giác OAH là tam giác đều nên góc OAH = góc OHA = 60 độ. Do tam giác ABC là tam giác cân tại A nên góc ABC = góc ACB. Mà góc OAH = góc ABC nên điểm E nằm trên đường tròn tâm O đường kính AH.