5. Cho nửa đường tròn tâm O, đường kính AB. Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến d của...
Câu hỏi:
5. Cho nửa đường tròn tâm O, đường kính AB. Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến d của nửa đường tròn. Gọi E, F lần lượt là chân các đường vuông góc kẻ từ A và B đến đường thẳng d. H là hình chiếu của M trên AB.
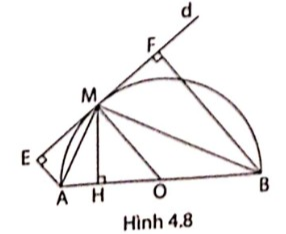
Chứng minh rằng:
a, ME = MF
b, AM là tia phân giác của góc BAE.
c, AE = AH
d, MH$^{2}$ = AE.BF
Câu trả lời:
Người trả lời: GV. Đỗ Văn Linh
Phương pháp giải:a. Ta có $AE \perp EF$ và $BF \perp EF$ => Tứ giác AEFB là hình thang vuông.Do đường d là tiếp tuyến của nửa đường tròn tại M, suy ra tứ giác AEMF là hình bình hành.Vậy, $ME = MF$.b. Ta có tam giác OMA cân tại O (OA = OM).Đồng thời, ta cũng có $OM \parallel AE \parallel BF$ (do cùng vuông góc với EF).Vậy M là trung điểm của EF, nên $ME = MF$.c. Ta có tam giác EAM và HAM đều vuông tại E và H.Với $EA = HA$ và $\angle EAM = \angle HAM$, ta suy ra tam giác EAM và HAM đồng dạng.Do đó, ta có $AE = AH$.d. Chứng minh tương tự phần b và c, ta cũng suy ra $MH^2 = AE \cdot BF$.Vậy, câu trả lời cho câu hỏi trên là:a. $ME = MF$b. $AM$ là tia phân giác của góc $BAE$c. $AE = AH$d. $MH^2 = AE \cdot BF$
Câu hỏi liên quan:
- 1. a, Sau khi vẽ đường thẳng d và đường tròn (O) như hình 4.5 bạn Hiền liền nhận xét: "Đường thẳng...
- 2. Cho tam giác ABC cân tại A, I là giao điểm của các đường phân giác.a, Hãy xác định vị trí tương...
- 3. Cho đoạn thẳng AB. Đường tròn tâm O, đường kính 3 cm tiếp xúc với đường thẳng AB. Tâm O...
- 4. Cho đường tròn (O), bán kính OM, dây CD là đường trung trực của OM (hình 4.7).a, Tứ giác OCMD là...






d. Áp dụng định lý đường tròn nội tiếp, ta có MH^2 = MA.MB = AE.BF.
c. Gọi K là hình chiếu của M trên BF, ta có tứ giác AKFH và tứ giác AEIH đều là tứ giác nội tiếp (do có 4 điểm thẳng hàng). Suất ra từ đó ta có AE = AH.
b. Gọi I là giao điểm của AM và BF, ta có góc AIB = góc MAB = góc MFB (do cùng chứng minh được với góc trực diện) nên tứ giác ABIF là tứ giác nội tiếp. Từ đó, AM là tia phân giác của góc BAE.
a. Ta có MH là đường cao của tam giác MEF nên ME = MF theo tính chất của tam giác vuông.