4. Cho đường tròn (O), bán kính OM, dây CD là đường trung trực của OM (hình 4.7).a, Tứ giác OCMD là...
Câu hỏi:
4. Cho đường tròn (O), bán kính OM, dây CD là đường trung trực của OM (hình 4.7).
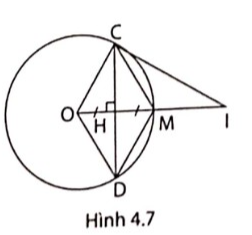
a, Tứ giác OCMD là hình gì? Giải thích câu trả lời của em.
b, Kẻ tiếp tuyến với đường tròn O tại C, tiếp tuyến này cắt đường thẳng OM tại I. Tính độ dài đoạn thẳng CI, biết OC = $2\sqrt{3}$(cm)
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Vương
a, Phương pháp giải:- Xét tam giác OCD cân tại O (OC = OD), có OH là đường cao => OH cũng là đường trung trực => HC = HD.- Tứ giác OCMD có OM vuông góc với CD và cắt nhau tại trung điểm của mỗi đường => OCMD là hình thoi.Câu trả lời: Tứ giác OCMD là hình thoi.b,Phương pháp giải:- Vì OCMD là hình thoi nên CM = OC => Tam giác OCM đều (OC = OM = MC).- Vì CI là tiếp tuyến của đường tròn O tại C => OC vuông góc CI.- Xét tam giác vuông OCI có CI = OC.tan∠COI = $2\sqrt{3}$.tan60° = 6 cm.Câu trả lời: Độ dài đoạn thẳng CI là 6 cm.
Câu hỏi liên quan:
- 1. a, Sau khi vẽ đường thẳng d và đường tròn (O) như hình 4.5 bạn Hiền liền nhận xét: "Đường thẳng...
- 2. Cho tam giác ABC cân tại A, I là giao điểm của các đường phân giác.a, Hãy xác định vị trí tương...
- 3. Cho đoạn thẳng AB. Đường tròn tâm O, đường kính 3 cm tiếp xúc với đường thẳng AB. Tâm O...
- 5. Cho nửa đường tròn tâm O, đường kính AB. Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến d của...






b, Ta có CI^2 = OM * IM (vì I là tiếp điểm của tiếp tuyến với đường tròn). Do đó, ta có CI^2 = OC^2 - OM^2 = (2√3)^2 - OM^2. Đồng thời, ta có OC = 2OM (vì dây CD là đường trung trực của OM), nên CI^2 = 12 - OM^2. Với OM là bán kính của đường tròn, ta có CI^2 = 12 - 4^2. Từ đó suy ra CI = √8 = 2√2.
a, Tứ giác OCMD là hình chữ nhật. Vì OC = MD (vì CD là đường trung trực của OM), và OMC = 90 độ (do CD là tiếp tuyến của đường tròn), nên OCMD là hình chữ nhật.
a, Tứ giác OCMD là hình vuông. Do CD là đường trung trực của OM nên OMC = 90 độ. Từ đó suy ra OCMD là hình vuông.