2. Cho tam giác ABC cân tại A, I là giao điểm của các đường phân giác.a, Hãy xác định vị trí tương...
Câu hỏi:
2. Cho tam giác ABC cân tại A, I là giao điểm của các đường phân giác.
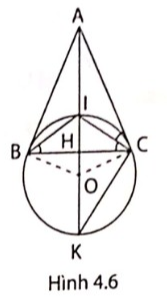
a, Hãy xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp tam giác BIC.
b, Gọi H là trung điểm của BC, IK là đường kính của đường tròn (O). Chứng minh rằng: $\frac{AI}{AK}=\frac{HI}{HK}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Vương
Phương pháp giải:a, Ta chứng minh được đường tròn (O) ngoại tiếp tam giác BIC có tâm O và tâm đường tròn này nằm trên đường thẳng IO, suy ra ba điểm A, I, O thẳng hàng. Sau đó chứng minh được đường thẳng AC là tiếp tuyến của đường tròn (O) tại điểm C.b, Ta có $\widehat{OIC}$ = $\widehat{ICB}$ (tam giác cân tại I) và $\widehat{OCI}$ = $\widehat{OIC}$ (vì OI = OC), suy ra tam giác OIC cũng cân tại O. Do đó, ta có $\widehat{OCA}$ = 90°, từ đó suy ra AC tiếp xúc với đường tròn (O) tại C.Câu trả lời: $\frac{AI}{AK}=\frac{HI}{HK}$
Câu hỏi liên quan:
- 1. a, Sau khi vẽ đường thẳng d và đường tròn (O) như hình 4.5 bạn Hiền liền nhận xét: "Đường thẳng...
- 3. Cho đoạn thẳng AB. Đường tròn tâm O, đường kính 3 cm tiếp xúc với đường thẳng AB. Tâm O...
- 4. Cho đường tròn (O), bán kính OM, dây CD là đường trung trực của OM (hình 4.7).a, Tứ giác OCMD là...
- 5. Cho nửa đường tròn tâm O, đường kính AB. Qua điểm M thuộc nửa đường tròn, kẻ tiếp tuyến d của...






{ "content1": "a. Để xác định vị trí tương đối của đường thẳng AC với đường tròn (O) ngoại tiếp tam giác BIC, ta có thể sử dụng tính chất của góc ở tâm và góc ngoài tiếp của tam giác. Trong trường hợp này, góc BIC là góc ngoại tiếp của tam giác ABC nên góc BIC = 2*góc BAC. Vì tam giác ABC cân tại A nên góc BAC = 90 độ, suy ra góc BIC = 180 độ. Do đó, đường AC sẽ tiếp xúc với đường tròn (O) tại điểm I.", "content2": "b. Để chứng minh $\frac{AI}{AK}=\frac{HI}{HK}$, ta quan sát tứ giác AIHK. Ta có $\widehat{AIH}=\widehat{AKH}=90^{\circ}$ (do HA là đường phân giác của góc ABC cân tại A). Từ đó, ta nhận thấy tứ giác AIHK là tứ giác hình vuông với các đường chéo là AI và HK. Do đó, $\frac{AI}{AK}=\frac{HI}{HK}$.", "content3": "c. Một cách khác để chứng minh $\frac{AI}{AK}=\frac{HI}{HK}$ là sử dụng định lí Sin trong tam giác vuông AIH và AKH. Ta có $\frac{AI}{AK}=\frac{sin\widehat{AKI}}{sin\widehat{AIK}}$ và $\frac{HI}{HK}=\frac{sin\widehat{HKI}}{sin\widehat{HIK}}$. Từ đó, ta cần chứng minh $\frac{sin\widehat{AKI}}{sin\widehat{AIK}}=\frac{sin\widehat{HKI}}{sin\widehat{HIK}}$."}