5. Cho nửa đường tròn tâm O đường kính AB, dây CD khác AB. Gọi I là hình chiếu của O trên dây CD.a,...
Câu hỏi:
5. Cho nửa đường tròn tâm O đường kính AB, dây CD khác AB. Gọi I là hình chiếu của O trên dây CD.
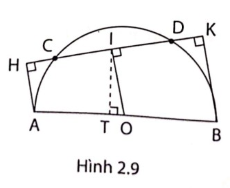
a, Chứng minh rằng I là trung điểm của CD
b, Gọi H, K theo thứ tự là chân các đường vuông góc kẻ từ A, B đến CD. Chứng minh rằng I là trung điểm của HK.
c, Gọi T là hình chiếu của I trên AB. Chứng minh rằng SACB + SADB = IT.AB
d, Tìm vị trí của dây CD để diện tích tứ giác AHKB là lớn nhất.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Đạt
Phương pháp giải:
a, Ta chứng minh được rằng I là trung điểm của CD bằng cách chứng minh rằng tam giác OCD là tam giác cân tại O và OI là đường cao của tam giác này.
b, Chứng minh I là trung điểm của HK bằng cách chứng minh rằng AH // BK // OI và OI là trung tuyến của tam giác AHKB.
c, Chứng minh diện tích tổng của hai tam giác SACB và SADB bằng diện tích tứ giác ITAB.
d, Để diện tích tứ giác AHKB là lớn nhất, dây CD cần nằm song song với AB.
Câu trả lời:
a, I là trung điểm của CD vì tam giác OCD là tam giác cân tại O và OI là đường cao của tam giác này.
b, I là trung điểm của HK do tam giác AHKB là hình thang và OI là trung tuyến của nó.
c, Diện tích tổng của hai tam giác SACB và SADB bằng diện tích tứ giác ITAB.
d, Dây CD cần nằm song song với AB đẻ diện tích tứ giác AHKB là lớn nhất.
a, Ta chứng minh được rằng I là trung điểm của CD bằng cách chứng minh rằng tam giác OCD là tam giác cân tại O và OI là đường cao của tam giác này.
b, Chứng minh I là trung điểm của HK bằng cách chứng minh rằng AH // BK // OI và OI là trung tuyến của tam giác AHKB.
c, Chứng minh diện tích tổng của hai tam giác SACB và SADB bằng diện tích tứ giác ITAB.
d, Để diện tích tứ giác AHKB là lớn nhất, dây CD cần nằm song song với AB.
Câu trả lời:
a, I là trung điểm của CD vì tam giác OCD là tam giác cân tại O và OI là đường cao của tam giác này.
b, I là trung điểm của HK do tam giác AHKB là hình thang và OI là trung tuyến của nó.
c, Diện tích tổng của hai tam giác SACB và SADB bằng diện tích tứ giác ITAB.
d, Dây CD cần nằm song song với AB đẻ diện tích tứ giác AHKB là lớn nhất.
Câu hỏi liên quan:
- 1. Cho đường tròn (Q). Tìm x trong những trường hợp dưới đây (Hình 2.5):
- 2. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm bất kì thuộc cung BC không chứa A. Gọi...
- 3. Hai bạn Hà và Châu viết kết luận về các dây cung của đường tròn (F) vào các tờ giấy dưới đây. Em...
- 4. Trong một bản tin thời sự có phát thông tin về một vụ tai nạn giao thông trên núi. Theo lời nhân...






d. Để diện tích tứ giác AHKB lớn nhất, dây CD cần đi qua tâm O của nửa đường tròn. Khi đó, tứ giác AHKB sẽ là hình bình hành có diện tích lớn nhất.
c. Diện tích của tứ giác SADB là diện tích hình chữ nhật ADBO, diện tích của tứ giác SACB là diện tích hình chữ nhật ACBO và diện tích của ITAB là diện tích hình chữ nhật IATB. Vì I là trung điểm của AB nên diện tích của ITAB bằng 1/2 diện tích hình chữ nhật ADBO. Từ đó, ta có SACB + SADB = ITAB = 1/2 SADB.
b. Vì H, K lần lượt là chân đường vuông góc từ A, B đến CD nên AHKB là hình bình hành. Do đó, I là trung điểm của các đường chéo của hình bình hành nên I là trung điểm của HK.
a. Ta có O là tâm của nửa đường tròn, do đó I là hình chiếu của O trên dây CD nên I là trung điểm của CD (vì hình chiếu của tâm trên dây của nửa đường tròn là trung điểm của dây đó).