2. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm bất kì thuộc cung BC không chứa A. Gọi...
Câu hỏi:
2. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm bất kì thuộc cung BC không chứa A. Gọi D, E theo thứ tự là các điểm đối xưng với M qua AB, AC (hình 2.6).
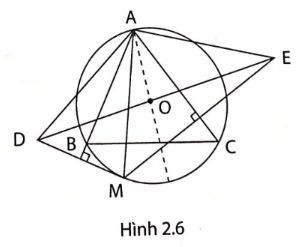
a, Chứng minh rằng tam giác ADM và tam giác AME là các tam giác cân.
b, Chứng minh rằng $\widehat{DAE}=2\widehat{BAC}$
c, Gọi H là hình chiếu của A trên DE. Đặt $\widehat{HAE}=\alpha $. Viết biểu thức thể hiện mối liên hệ giữa $\alpha $, AE và DE.
d, Tìm vị trí của M trên cung BC để DE có độ dài lớn nhất.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Vương
Để giải bài toán trên, ta có các bước sau:a. Chứng minh tam giác ADM và tam giác AME là các tam giác cân:- D đối xứng với M qua AB, suy ra AB vuông góc với DM. - AB là đường trung tuyến của tam giác ADM, do đó tam giác ADM cân tại A.- Tương tự, ta chứng minh được rằng tam giác AME cũng cân tại A.b. Chứng minh $\widehat{DAE}=2\widehat{BAC}$:- Do tam giác ADM cân tại A, ta có $\widehat{DAB} = \widehat{BAM} = \frac{1}{2} \widehat{DAM}$.- Đồng thời, tam giác AME cũng cân tại A, nên $\widehat{MAC} = \widehat{CAE} = \frac{1}{2} \widehat{MAE}$.- Từ đó, suy ra $\widehat{DAE} = \widehat{DAB} + \widehat{BAM} + \widehat{MAC} + \widehat{CAE} = 2\widehat{BAM} + 2\widehat{MAC} = 2(\widehat{BAM} + \widehat{MAC}) = 2\widehat{BAC}$.c. Viết biểu thức thể hiện mối liên hệ giữa $\alpha$, AE và DE:- Ta có HE = AE.sin$\alpha$, suy ra DE = 2AE.sin$\alpha$.d. Để DE đạt độ dài lớn nhất, ta cần chọn vị trí của M sao cho AM là đường kính của đường tròn (hay A, O, M thẳng hàng).Với các bước trên, ta đã giải được bài toán. Để trả lời chi tiết và đầy đủ hơn, bạn có thể xem lại các bước trên và trình bày cụ thể hơn.
Câu hỏi liên quan:
- 1. Cho đường tròn (Q). Tìm x trong những trường hợp dưới đây (Hình 2.5):
- 3. Hai bạn Hà và Châu viết kết luận về các dây cung của đường tròn (F) vào các tờ giấy dưới đây. Em...
- 4. Trong một bản tin thời sự có phát thông tin về một vụ tai nạn giao thông trên núi. Theo lời nhân...
- 5. Cho nửa đường tròn tâm O đường kính AB, dây CD khác AB. Gọi I là hình chiếu của O trên dây CD.a,...






{ "content1": "a. Ta có: AD = DM (do D là điểm đối xứng với M qua AB) và AE = EM (do E là điểm đối xứng với M qua AC). Vậy tam giác ADM và tam giác AME là các tam giác cân.", "content2": "b. Ta có: $\widehat{DAM} = \widehat{EAM}$ (cùng là góc lần lượt ở chân tam giác cân ADM và AME), $\widehat{DAB} = \widehat{EAC}$ (cùng là góc ngoại tiếp trong của tam giác ABC). Do đó, $\widehat{DAE} = 2\widehat{BAC}$.", "content3": "c. Ta có: $\widehat{HAE} = \alpha$ và $\widehat{HDA} = 90^\circ$ (do H là hình chiếu của A trên DE). Từ đó suy ra: $\alpha + \widehat{DAE} = 90^\circ$.", "content4": "d. Để DE có độ dài lớn nhất, ta cần tìm vị trí của M sao cho đường thẳng DM cũng chính là đường thẳng vuông góc với DE. Điều này xảy ra khi M là trung điểm của BC (vị trí M sao cho DM vuông góc với DE và DE là phân giác của góc BMC)."}