3. Hai bạn Hà và Châu viết kết luận về các dây cung của đường tròn (F) vào các tờ giấy dưới đây. Em...
Câu hỏi:
3. Hai bạn Hà và Châu viết kết luận về các dây cung của đường tròn (F) vào các tờ giấy dưới đây. Em hãy cho biết bạn nào viết đúng. Giải thích.
| Hình vẽ | Hà | Châu |
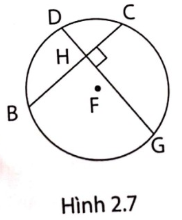 | Vì DG $\perp $ BC nên DG là đường trung trực của BC | Tuy DG $\perp $ BC, nhưng DG không là đường trung trực của BC vì DG không là đường kính. |
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Huy
Để giải bài toán này, ta cần sử dụng kiến thức về hình học đường tròn và đường kính của đường tròn.Phương pháp giải:- Châu viết rằng "DG không là đường trung trực của BC vì DG không là đường kính". Điều này không đúng vì trong một đường tròn, đường trung trực của một cung không nhất thiết phải là đường kính của đường tròn. Vì vậy, lý do Châu đưa ra là không chính xác.- Hà viết rằng "Vì DG $\perp $ BC nên DG là đường trung trực của BC". Điều này cũng không chính xác vì để DG là đường trung trực của BC, H cần chứng minh thêm rằng DG cắt BC tại trung điểm. Vì vậy, lý do mà Hà đưa ra cũng không chính xác.Câu trả lời:Dựa vào phương pháp giải trên, ta đưa ra câu trả lời là cả hai bạn đều viết không đúng vì cần phải có bằng chứng rõ ràng để đưa ra kết luận về tính chất của dây cung và đường trung trực của đường tròn.
Câu hỏi liên quan:
- 1. Cho đường tròn (Q). Tìm x trong những trường hợp dưới đây (Hình 2.5):
- 2. Cho tam giác ABC nhọn nội tiếp đường tròn (O). M là điểm bất kì thuộc cung BC không chứa A. Gọi...
- 4. Trong một bản tin thời sự có phát thông tin về một vụ tai nạn giao thông trên núi. Theo lời nhân...
- 5. Cho nửa đường tròn tâm O đường kính AB, dây CD khác AB. Gọi I là hình chiếu của O trên dây CD.a,...






Châu viết đúng vì DG không thể là đường trung trực của BCD nếu không là đường kính của đường tròn
Hà viết đúng vì DG nằm trên đường trung trực của tam giác BCD
Châu viết đúng vì để DG là đường trung trực thì DG phải đi qua trung điểm của BC
Hà viết đúng vì dù DG không phải là đường kính nhưng vẫn có thể là đường trung trực của tam giác BCD
Châu viết đúng vì để DG là đường trung trực của tam giác BCD thì DG phải là đường kính của đường tròn