5. Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD với A, C...
Câu hỏi:
5. Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD với A, C thuộc (O) và B, D thuộc (O') (hình 7.9).
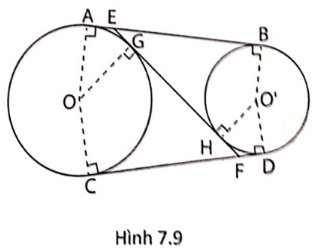
a, Chứng minh rằng AB và CD đối xứng với nhau qua OO'.
b, Tiếp tuyến chung trong GH cắt AB và CD theo thứ tự tại E và F với G thuộc (O), H thuộc (O'). Chứng minh rằng AE = EG và EB = EH.
c, Chứng minh rằng EG = FH, AB = EF.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Phương
Phương pháp giải câu hỏi trên như sau:a. Ta chứng minh được AB và CD đối xứng với nhau qua OO' bằng cách chứng minh A và B đối xứng với nhau qua OO', cũng như C và D đối xứng với nhau qua OO'.b. Chứng minh AE = EG và EB = EH bằng tính chất của hai tiếp tuyến cắt nhau của các đường tròn. c. Chứng minh EG = FH và AB = EF bằng cách sử dụng phép cộng hai phía và tính chất của đối xứng và tiếp tuyến cắt nhau.Câu trả lời cho câu hỏi trên: a. AB và CD đối xứng với nhau qua OO'.b. AE = EG, EB = EH.c. EG = FH, AB = EF.
Câu hỏi liên quan:
- 1.Ở hình 7.5, các điểm L, Q, N và P đều là các tiếp điểm của đường tròn (C) và (D). Biết rằng...
- 2. Phần lớn các đĩa nhạc CD hiện nay đều có ba đường tròn đồng tâm. Đường tròn thứ nhất là lỗ hổng...
- 3. Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC với điểm...
- 4. Cho hai đường tròn (O) và (O') có cùng bán kính. Gọi A, B là giao điểm của hai đường tròn. Qua A...






a, Chứng minh AB và CD đối xứng qua OO': Gọi M là trung điểm của OO'. Khi đó ta có M là trung điểm của đoạn thẳng AB và CD. Do đó, AB và CD đối xứng qua trục đối xứng OO'.
c, Ta có các tam giác EAG và EIH đồng dạng do chúng có các góc tương đồng. Từ đó suy ra EG = IH. Kết hợp với điều kiện trên, ta có EG = FH và từ ba điểm G, E, F thuộc cùng một đường thẳng, suy ra AB = EF.
b, Gọi I là giao điểm của AB và CD. Ta có các tam giác AGI và HBI đồng dạng với các góc ở trung điểm của hai tiếp tuyến với một đường thẳng và một đường tròn. Từ đó suy ra AE = EG và EB = EH.
a, Ta có AB và CD là hai tiếp tuyến chung ngoài của hai đường tròn (O) và (O'), do đó chúng đối xứng qua trung điểm của đoạn thẳng OO'.