1.Ở hình 7.5, các điểm L, Q, N và P đều là các tiếp điểm của đường tròn (C) và (D). Biết rằng...
Câu hỏi:
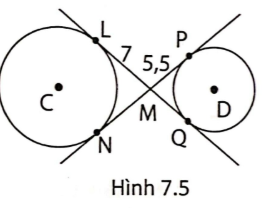
1. Ở hình 7.5, các điểm L, Q, N và P đều là các tiếp điểm của đường tròn (C) và (D). Biết rằng LM = 7 và MP = 5,5. Tìm độ dài các đoạn thẳng LQ và NP.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Giang
Phương pháp giải:
- Ta có MN = ML = 7 và MQ = MP = 5,5
- Vì ML và MN là hai tiếp tuyến cắt nhau tại M của đường tròn (C) nên MN = ML = 7
- Vì MQ và MP là hai tiếp tuyến cắt nhau tại M của đường tròn (D) nên MQ = MP = 5,5
- Ta có LQ = ML + MQ = 7 + 5,5 = 12,5
- Ta có NP = NM + MP = 7 + 5,5 = 12,5
Vậy, độ dài của các đoạn thẳng LQ và NP lần lượt là 12,5 đơn vị.
- Ta có MN = ML = 7 và MQ = MP = 5,5
- Vì ML và MN là hai tiếp tuyến cắt nhau tại M của đường tròn (C) nên MN = ML = 7
- Vì MQ và MP là hai tiếp tuyến cắt nhau tại M của đường tròn (D) nên MQ = MP = 5,5
- Ta có LQ = ML + MQ = 7 + 5,5 = 12,5
- Ta có NP = NM + MP = 7 + 5,5 = 12,5
Vậy, độ dài của các đoạn thẳng LQ và NP lần lượt là 12,5 đơn vị.
Câu hỏi liên quan:
- 2. Phần lớn các đĩa nhạc CD hiện nay đều có ba đường tròn đồng tâm. Đường tròn thứ nhất là lỗ hổng...
- 3. Cho hai đường tròn (O; R) và (O'; r) tiếp xúc ngoài tại A. Kẻ tiếp tuyến chung ngoài BC với điểm...
- 4. Cho hai đường tròn (O) và (O') có cùng bán kính. Gọi A, B là giao điểm của hai đường tròn. Qua A...
- 5. Cho hai đường tròn (O) và (O') ở ngoài nhau. Kẻ các tiếp tuyến chung ngoài AB và CD với A, C...






Áp dụng định lý đường tròn nội tiếp, ta có MQ*MN = NP*LP. Từ đó suy ra MN = 14 và LP = 11. Ta có MQ = 11/2 và MP = MQ + 5.5 = 16.5. Kết hợp với MN = 14, suy ra LQ = 22 và NP = 22.
Gọi G là điểm giao điểm của MN và LP. Ta có LM*MQ = LQ*QP (theo định lí đường tròn nội tiếp). Khi đó, ta có MQ = 11/2 và MP = 11/2 + 5.5 = 16.5. Suy ra LQ = 22 và NP = 22.
Gọi O là tâm của đường tròn (C) và (D). Khi đó, ta có LQ = 2*R, trong đó R là bán kính của đường tròn. Theo định lý đường tròn nội tiếp, ta có LM*MQ = LQ*QP. Từ đó suy ra R = 11 và vậy LQ = 22.