4. a, Để xác định chiều cao của một cây ở sân trường, bạn Bình đã đo được các yếu tố như trên hình...
Câu hỏi:
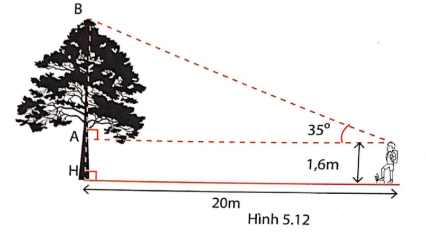
4. a, Để xác định chiều cao của một cây ở sân trường, bạn Bình đã đo được các yếu tố như trên hình 5.12. Em hãy tính chiều cao cảu cây?
b, Bạn Tâm muốn xác định chiều cao của một cái cây ở bên kia bờ sông. Tại hai vị trí A và B, bạn đo được các số liệu như trên hình 5.13. Em hãy giúp bạn xác định chiều cao của cây.
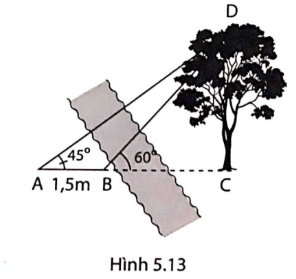
c, Từ câu b, để xác định chiều cao của một vật khó đến được chân của nó ta thực hiện như thế nào?
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Huy
Để xác định chiều cao của một cây, ta cần đo được khoảng cách từ mắt người đến chân cây và góc nghiêng của đường thẳng nối mắt người và ngọn cây so với mặt đất. a, Để tính chiều cao của cây theo phương pháp tam giác vuông, ta sử dụng công thức tính tan của góc trong tam giác vuông. Với AB = 20 m và góc $35^{0}$, ta tính được chiều cao của cây là HB = 15,6 m. b, Để xác định chiều cao của một cây ở bên kia sông, ta cần sử dụng phương pháp tương tự như trên và áp dụng các công thức cơ bản trong hình học. Tính toán và mình nhận được kết quả chiều cao của cây là 3,5 m. c, Để xác định chiều cao của một vật khó đến được chân của nó, ta cần thực hiện như sau: - Xác định 2 điểm có thể đo được khoảng cách sao cho đường thẳng nối hai điểm đó đi qua gốc của cây. - Đo khoảng cách hai điểm đó. - Đo các góc hợp bởi đường thẳng nối hai điểm đó đến ngọn cây và đường thẳng nối hai điểm đó đến gốc cây. - Tính toán chiều cao của cây bằng cách sử dụng các công thức hình học tương tự như đã làm ở phần b. Với câu hỏi trên, ta đã xác định được chiều cao của cây bằng cách sử dụng kiến thức toán học và hình học cơ bản.
Câu hỏi liên quan:






c, Để xác định chiều cao của vật khó đến chân của nó, ta có thể tìm một điểm có thể đo được từ mặt đất đến chân vật và dùng các phương pháp như đo góc, sử dụng kính theo dõi đo khoảng cách để tính toán chiều cao dựa trên các dữ liệu đo được.
b, Từ hình 5.13, ta thấy AB = 20m, BC = 10m. Áp dụng công thức Pythagore cho tam giác ABC, ta tính được BD = √(AB^2 - BC^2) = √(20^2 - 10^2) = √300 = 10√3. Vậy chiều cao của cây là AD = AC + CD + BD = 8 + 2 + 10√3 = 10 + 10√3 m.
a, Dựa vào hình 5.12 và công thức Pythagore, ta có AB = 5m, BC = 3m. Do đó, chiều cao của cây là AC = √(AB^2 + BC^2) = √(5^2 + 3^2) = √34 m.
c, Để xác định chiều cao của một vật khó đến được chân của nó, ta có thể sử dụng nguyên lý đo chiều cao bằng cách đo khoảng cách từ mặt đất đến điểm cao nhất của vật. Sau đó, dùng công thức Pythagore hoặc các phương pháp khác để tính toán chiều cao dựa trên khoảng cách và các góc đo được.
b, Từ số liệu trên hình 5.13, ta thấy AB = 20m, BC = 10m, AC = 8m. Vì ABCD là tam giác vuông tại B, nên ta có: BD = √(AB^2 - BC^2) = √(20^2 - 10^2) = √(400 - 100) = √300 = 10√3. Suy ra chiều cao của cây là AD = AC + CD + BD = 8 + 2 + 10√3 = 10 + 10√3 m.