6. Đồ thị và tính chất của hàm số y = cotxHoạt động 7 trang 29 sách giáo khoa (SGK) toán lớp 11 tập...
Câu hỏi:
6. Đồ thị và tính chất của hàm số y = cotx
Hoạt động 7 trang 29 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hàm số y = cot x.
a) Xét tính chẵn, lẻ của hàm số.
b) Hoàn thành bảng giá trị sau của hàm số y = cot x trên khoảng (0; π).
| x | $\frac{\pi }{6}$ | $\frac{\pi }{4}$ | $\frac{\pi }{3}$ | $\frac{\pi }{2}$ | $\frac{2\pi }{3}$ | $\frac{3\pi }{4}$ | $\frac{5\pi }{6}$ |
| y=cotx | ? | ? | ? | ? | ? | ? | ? |
Bằng cách lấy nhiều điểm M(x; cot x) với x ∈ (0; π) và nối lại ta được đồ thị hàm số y = cot x trên khoảng (0; π).
c) Bằng cách làm tương tự câu b cho các khoảng khác có độ dài bằng chu kì T = π, ta được đồ thị của hàm số y = cot x như hình dưới đây.
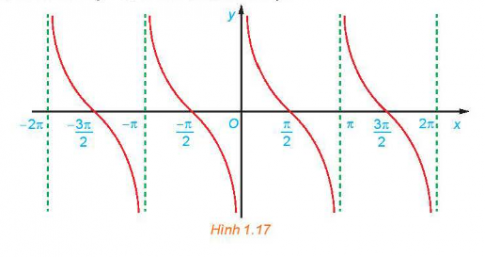
Từ đồ thị ở Hình 1.17, hãy tìm tập giá trị và các khoảng nghịch biến của hàm số y = cotx.
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ánh
Trong bài toán này, chúng ta cần xác định tính chẵn, lẻ của hàm số y = cot x, hoàn thành bảng giá trị trên khoảng (0; π) và tìm tập giá trị và các khoảng nghịch biến của hàm số y = cot x.a) Tính chẵn, lẻ của hàm số y = cot x:- Ta có: y = cot x- F(-x) = cot (-x) = -cot x = -f(x), với x thuộc tập xác định D = ℝ \ {kπ | k ∈ Z}Do đó, hàm số y = cot x là hàm số lẻ.b) Hoàn thành bảng giá trị của hàm số y = cot x trên khoảng (0; π):- Tính các giá trị của cot x ứng với các giá trị của x là $\frac{\pi}{6}, \frac{\pi}{4}, \frac{\pi}{3}, \frac{\pi}{2}, \frac{2\pi}{3}, \frac{3\pi}{4}, \frac{5\pi}{6}$- Lấy các giá trị của tan x từ bảng tan x = $\sqrt{3}, 1, \frac{\sqrt{3}}{3}, 0, -\frac{\sqrt{3}}{3}, -1, -\sqrt{3}$- Từ đó, hoàn thành bảng giá trị như sau:x $\frac{\pi}{6}$ $\frac{\pi}{4}$ $\frac{\pi}{3}$ $\frac{\pi}{2}$ $\frac{2\pi}{3}$ $\frac{3\pi}{4}$ $\frac{5\pi}{6}$y = cot x $\sqrt{3}$ 1 $\frac{\sqrt{3}}{3}$ 0 $-\frac{\sqrt{3}}{3}$ -1 $-\sqrt{3}$c) Tập giá trị và các khoảng nghịch biến của hàm số y = cot x:- Ta quan sát đồ thị của hàm số y = cot x và xác định:+ Tập giá trị là ℝ+ Hàm số đồng biến trên mỗi khoảng $(k\pi; \pi + k\pi), k ∈ Z$ (do đồ thị hàm số đi lên từ trái sang phải trên mỗi khoảng này).Vậy đó là cách giải toán 6 trong sách giáo khoa Toán lớp 11, tìm tính chất, bảng giá trị và tập giá trị của hàm số y = cot x, hy vọng bạn sẽ hiểu rõ phần này.
Câu hỏi liên quan:
- 1. Định nghĩa hàm số lượng giácHoạt động 1 trang 22 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:...
- Luyện tập 1 trang 23 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập xác định của hàm số...
- 2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoànHoạt động 2 trang 23 sách giáo khoa (SGK) toán lớp 11...
- Luyện tập 2 trang 24 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tính chẵn, lẻ của hàm...
- Hoạt động 3 trang 24 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:So sánh:a) sin(x + 2π) và...
- Câu hỏi trang 24 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Hàm số hằng f(x) = c (c là hằng...
- Luyện tập 3 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tính tuần hoàn của hàm...
- 3. Đồ thị và tính chất của hàm số y = sinxHoạt động 4 trang 25 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 4 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập giá trị của hàm số y...
- Vận dụng 1 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tình huống mở đầu.a) Giải...
- 4. Đồ thị và tính chất của hàm số y = cosxHoạt động 5 trang 26 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 5 trang 27 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập giá trị của hàm số y...
- Vận dụng 2 trang 27 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Trong Vật lí, ta biết rằng...
- 5. Đồ thị và tính chất của hàm số y = tanxHoạt động 6 trang 28 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 6 trang 29 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Sử dụng đồ thị đã vẽ ở Hình...
- Luyện tập 7 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Sử dụng đồ thị đã vẽ ở Hình...
- Bài tậpBài tập 1.14 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập xác định của...
- Bài tập 1.15 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tính chẵn lẻ của các...
- Bài tập 1.16 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập giá trị của các hàm...
- Bài tập 1.17 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Từ đồ thị của hàm số y =...
- Bài tập 1.18 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Giả sử khi một cơn sóng...
Bình luận (0)





