2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoànHoạt động 2 trang 23 sách giáo khoa (SGK) toán lớp 11...
Câu hỏi:
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
Hoạt động 2 trang 23 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT: Cho hai hàm số $f(a)=x^{2}$ và $g(x)=x^{3}$, với các đồ thị như hình dưới đây
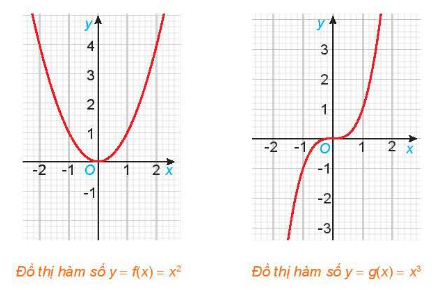
a) Tìm các tập xác định D1, Dg của các hàm số f(x) và g(x)
b) Chứng tỏ rằng $f(-x) = f(x),\forall x\in Dg$. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục tọa độ Oxy?
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Đức
Phương pháp giải:a) Ta có $f(x) = x^{2}$ và $g(x) = x^{3}$ có nghĩa với mọi x ∈ ℝ, vì vậy tập xác định của $f(x)$ là Df = ℝ và tập xác định của $g(x)$ là Dg = ℝ.b) Để chứng minh $f(-x) = f(x)$, ta thay x bằng -x vào biểu thức $f(x) = x^{2}$, ta có: $f(-x) = (-x)^{2} = x^{2}$, vậy $f(-x) = f(x)$, với mọi x ∈ Df. Từ biểu đồ, ta thấy đồ thị của hàm số $f(x)$ đối xứng qua trục tung Oy.c) Để chứng minh $g(-x) = -g(x)$, ta thay x bằng -x vào biểu thức $g(x) = x^{3}$, ta có: $g(-x) = (-x)^{3} = -x^{3} = -g(x)$, với mọi x ∈ Dg. Từ biểu đồ, ta thấy đồ thị của hàm số $g(x)$ nhận gốc tọa độ O làm tâm đối xứng.Vậy câu trả lời đầy đủ và chi tiết cho câu hỏi trên là:a) Df = Dg = ℝb) $f(-x) = f(x),\forall x\in Df$ và đồ thị hàm số y = f(x) đối xứng qua trục tung Oy.c) $g(-x) = -g(x),\forall x\in Dg$ và đồ thị hàm số y = g(x) nhận gốc tọa độ O làm tâm đối xứng.
Câu hỏi liên quan:
- 1. Định nghĩa hàm số lượng giácHoạt động 1 trang 22 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:...
- Luyện tập 1 trang 23 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập xác định của hàm số...
- Luyện tập 2 trang 24 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tính chẵn, lẻ của hàm...
- Hoạt động 3 trang 24 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:So sánh:a) sin(x + 2π) và...
- Câu hỏi trang 24 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Hàm số hằng f(x) = c (c là hằng...
- Luyện tập 3 trang 25 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tính tuần hoàn của hàm...
- 3. Đồ thị và tính chất của hàm số y = sinxHoạt động 4 trang 25 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 4 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập giá trị của hàm số y...
- Vận dụng 1 trang 26 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tình huống mở đầu.a) Giải...
- 4. Đồ thị và tính chất của hàm số y = cosxHoạt động 5 trang 26 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 5 trang 27 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập giá trị của hàm số y...
- Vận dụng 2 trang 27 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Trong Vật lí, ta biết rằng...
- 5. Đồ thị và tính chất của hàm số y = tanxHoạt động 6 trang 28 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 6 trang 29 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Sử dụng đồ thị đã vẽ ở Hình...
- 6. Đồ thị và tính chất của hàm số y = cotxHoạt động 7 trang 29 sách giáo khoa (SGK) toán lớp 11 tập...
- Luyện tập 7 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Sử dụng đồ thị đã vẽ ở Hình...
- Bài tậpBài tập 1.14 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập xác định của...
- Bài tập 1.15 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Xét tính chẵn lẻ của các...
- Bài tập 1.16 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Tìm tập giá trị của các hàm...
- Bài tập 1.17 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Từ đồ thị của hàm số y =...
- Bài tập 1.18 trang 30 sách giáo khoa (SGK) toán lớp 11 tập 1 KNTT:Giả sử khi một cơn sóng...
Bình luận (0)





