Vận dụng 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt trước của một công trình xây...
Câu hỏi:
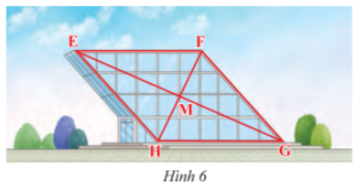
Vận dụng 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt trước của một công trình xây dựng được làm bằng kính có dạng hình bình hành EFGH với M là giao điểm của hai đường chéo (Hình 6). Cho biết EF = 40 m, EM = 36 m, HM = 16 m. Tính độ dài cạnh HG và độ dài hai đường chéo.
Câu trả lời:
Người trả lời: GV. Đỗ Văn Việt
Để tính độ dài cạnh HG và độ dài hai đường chéo của hình bình hành EFGH, ta có thể giải bằng cách sau:Cách 1:Vì EFGH là hình bình hành nên HG = EF = 40m.Ta có EM = 36m, HM = 16m. Gọi N là giao điểm của HF và EG.Theo định lý Pythagore trong tam giác EMH ta có:EH² = EM² + HM² = 36² + 16²Suy ra EH = √(36² + 16²) = √(1296 + 256) = √1552 ≈ 39.35mDo đó, ta có HN = EG - EH = 72m - 39.35m = 32.65mVậy ta có độ dài hai đường chéo là HG = 40m và HN = 32.65m.Cách 2:Vì EFGH là hình bình hành nên HG = EF = 40m.Ta có EM = 36m, HM = 16m. Gọi N là giao điểm của HF và EG.Ta có tam giác EMH vuông tại M nên ta có:EH = √(EM² + HM²) = √(36² + 16²) = √(1296 + 256) = √1552 ≈ 39.35mGọi x là độ dài HP. Khi đó, NP = EP - EN = 72m - 39.35m = 32.65mDo đó, ta có độ dài hai đường chéo là HG = 40m và HN = 32.65m.Vậy câu trả lời cho câu hỏi trên là: độ dài cạnh HG là 40m và độ dài hai đường chéo là 32.65m.
Câu hỏi liên quan:
- 1. Hình bình hànhThực hành 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình...
- Vận dụng 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mắt lưới của một lưới bóng chuyền...
- Thực hành 2 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các tứ giác ở Hình 9, tứ...
- Vận dụng 3 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát Hình 10, cho biết...
- 2. Hình thoiThực hành 3 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi MNPQ có...
- Vận dụng 4 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ dài cạnh của các khuy áo...
- Vận dụng 5 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một hoa văn trang trí được ghép bởi...
- Vận dụng 6 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một tứ giác có chu vi là 52 cm và...
- Bài tậpBài tập 1 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cần thêm một điều kiện gì để...
- Bài tập 2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD, kẻ AH vuông...
- Bài tập 3 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi E là...
- Bài tập 4 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD (AB...
- Bài tập 5 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD. Gọi I,...
- Bài tập 6 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình 21. Chứng minh rằng tứ...
- Bài tập 7 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thoi ABCD, hai đường...
- Bài tập 8 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC cân tại A, gọi...
- Bài tập 9 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm các hình bình hành và hình thang...
- Khởi động trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát hình chụp các mái nhà...
- Khám phá 1 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 1a là hình ảnh của một...
- Khám phá 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có các cạnh...
- Khám phá 3 trang 75 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có P là giao...
- Khám phá 4 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 11a là hình chụp tấm lưới...
- Khám phá 5 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Hình thoi có là hình bình...
- Khám phá 6 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho ABCD là một hình bình...






Kết quả tính toán cho độ dài cạnh HG và hai đường chéo của hình bình hành EFGH là: HG ≈ 48.82m, hai đường chéo ≈ 48.82m.
Cách khác để tính độ dài hai đường chéo của hình bình hành EFGH là sử dụng định lý Cosin trong tam giác vuông. Ta có: HG^2 = EH^2 + EF^2 - 2*EH*EF*cos(90°). Thay EH = 28 m, EF = 40 m vào công thức, ta suy ra HG = √(28^2 + 40^2 - 2*28*40*cos(90°)) ≈ 48.82m.
Để tính độ dài hai đường chéo của hình bình hành EFGH, ta sử dụng định lý Pythagoras trong tam giác vuông. Ta có: Số đo độ dài đường chéo là: d = √(EF^2 + EH^2) = √(40^2 + 28^2) = √(1600 + 784) = √2384 ≈ 48.82m.
Để tính độ dài cạnh HG, ta sử dụng định lý Pythagoras trong tam giác vuông. Vì MH là đường cao của tam giác vuông EMH nên ta có: EM^2 = EH^2 + HM^2. Thay EM = 36 m, HM = 16 m vào công thức ta có: 36^2 = EH^2 + 16^2. Tính được EH = 28 m. Do EFGH là hình bình hành nên HG = EF = 40 m.