Bài tập 6 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình 21. Chứng minh rằng tứ...
Câu hỏi:
Bài tập 6 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình 21. Chứng minh rằng tứ giác EFGH là hình thoi.
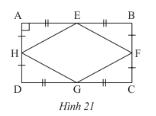
Câu trả lời:
Người trả lời: GV. Đỗ Thị Linh
Phương pháp giải:
- Ta có E là trung điểm của AB, F là trung điểm của BC, H là trung điểm của AD và G là trung điểm của DC.
- Do đó, ta có EF // AC và EF = 1/2 AC (1) và HG // AC và HG = 1/2 AC (2)
- Từ (1) và (2) suy ra EF // HG và EF = HG, vậy tứ giác EFGH là hình bình hành.
- Tứ giác ABCD có AB = CD và AD = BC nên ABCD là hình bình hành. Với $\widehat{BAD} = 90^{\circ}$ nên ABCD là hình chữ nhật.
- Xét ΔEBF và ΔCGF, ta có EB = EC (gt), BF = FC (gt) và $\widehat{EBF} = \widehat{GCF} = 90^{\circ}$
=> ΔEBF = ΔGCF (c.g.c) => EF = GF
- Chứng minh tương tự ta có GF = GH, GH = EF => EF = GF = GH = EH
- Do đó tứ giác EFGH là hình thoi.
Vậy, tứ giác EFGH là hình thoi.
- Ta có E là trung điểm của AB, F là trung điểm của BC, H là trung điểm của AD và G là trung điểm của DC.
- Do đó, ta có EF // AC và EF = 1/2 AC (1) và HG // AC và HG = 1/2 AC (2)
- Từ (1) và (2) suy ra EF // HG và EF = HG, vậy tứ giác EFGH là hình bình hành.
- Tứ giác ABCD có AB = CD và AD = BC nên ABCD là hình bình hành. Với $\widehat{BAD} = 90^{\circ}$ nên ABCD là hình chữ nhật.
- Xét ΔEBF và ΔCGF, ta có EB = EC (gt), BF = FC (gt) và $\widehat{EBF} = \widehat{GCF} = 90^{\circ}$
=> ΔEBF = ΔGCF (c.g.c) => EF = GF
- Chứng minh tương tự ta có GF = GH, GH = EF => EF = GF = GH = EH
- Do đó tứ giác EFGH là hình thoi.
Vậy, tứ giác EFGH là hình thoi.
Câu hỏi liên quan:
- 1. Hình bình hànhThực hành 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình...
- Vận dụng 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mắt lưới của một lưới bóng chuyền...
- Vận dụng 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt trước của một công trình xây...
- Thực hành 2 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các tứ giác ở Hình 9, tứ...
- Vận dụng 3 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát Hình 10, cho biết...
- 2. Hình thoiThực hành 3 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi MNPQ có...
- Vận dụng 4 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ dài cạnh của các khuy áo...
- Vận dụng 5 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một hoa văn trang trí được ghép bởi...
- Vận dụng 6 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một tứ giác có chu vi là 52 cm và...
- Bài tậpBài tập 1 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cần thêm một điều kiện gì để...
- Bài tập 2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD, kẻ AH vuông...
- Bài tập 3 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi E là...
- Bài tập 4 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD (AB...
- Bài tập 5 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD. Gọi I,...
- Bài tập 7 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thoi ABCD, hai đường...
- Bài tập 8 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC cân tại A, gọi...
- Bài tập 9 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm các hình bình hành và hình thang...
- Khởi động trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát hình chụp các mái nhà...
- Khám phá 1 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 1a là hình ảnh của một...
- Khám phá 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có các cạnh...
- Khám phá 3 trang 75 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có P là giao...
- Khám phá 4 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 11a là hình chụp tấm lưới...
- Khám phá 5 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Hình thoi có là hình bình...
- Khám phá 6 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho ABCD là một hình bình...






Do đó, ta có tứ giác EFGH là hình thoi với các cạnh bằng nhau và hai đường chéo cắt nhau vuông góc tại trọng tâm. Điều này chứng tỏ tứ giác EFGH là hình thoi.
Ta thấy EF song song với CD (vì E và F lần lượt là trung điểm của AB và CD) nên EF cũng song song với HG. Tương tự, ta có FG song song với AB nên FG cũng song song với EH.
Tương tự, F là trung điểm của CD nên FG cũng là cạnh trung bình của hình chữ nhật ABCD. Do đó, EG = FG.
Theo đề bài, hình 21 là hình chữ nhật ABCD và ta có E là trung điểm của AB. Khi đó, ta có EG là cạnh trung bình của hình chữ nhật ABCD.
Để chứng minh tứ giác EFGH là hình thoi, ta cần chứng minh rằng các cạnh của tứ giác này đều bằng nhau và hai đường chéo của nó cắt nhau vuông góc tại trọng tâm.