Khám phá 3 trang 75 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có P là giao...
Câu hỏi:
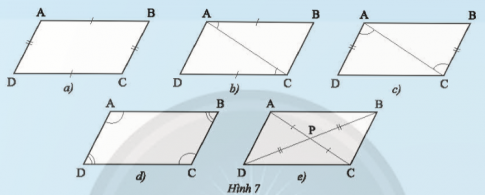
Khám phá 3 trang 75 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD có P là giao điểm của hai đường chéo. Giải thích tại sao AB // CD và AD // BC trong mỗi trường hợp sau:
Trường hợp 1: AB = CD và AD = BC (Hình 7a).
Trường hợp 2: AB // CD và AB = CD (Hình 7b).
Trường hợp 3: AD // BC và AD = BC (Hình 7c).
Trường hợp 4: $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ (Hình 7d).
Trường hợp 5: PA = PC, PB = PD (Hình 7e).
Câu trả lời:
Người trả lời: GV. Đỗ Thị Phương
Để giải câu hỏi này, ta có thể làm như sau:1. Ta xét từng trường hợp một: a. Trường hợp 1: Ta có AB = CD và AD = BC. Do đó tứ giác ABCD là tứ giác cân. Ta suy ra AB // CD và AD // BC. b. Trường hợp 2: Ta có AB // CD và AB = CD. Ta suy ra ABCD là hình bình hành, do đó AD // BC và AB // CD. c. Trường hợp 3: Ta có AD // BC và AD = BC. Ta suy ra ABCD là tứ giác cân. Do đó AB // CD và AD // BC. d. Trường hợp 4: Ta có $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$. Ta có tổng các góc trong tứ giác là 360 độ. Suy ra AD // BC và AB // CD. e. Trường hợp 5: Ta có PA = PC và PB = PD. Ta suy ra tứ giác PAB và PCD là tứ giác cân. Do đó AB // CD và AD // BC.Vậy là ta đã chứng minh được trong mỗi trường hợp đề cho, AB // CD và AD // BC.
Câu hỏi liên quan:
- 1. Hình bình hànhThực hành 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình...
- Vận dụng 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mắt lưới của một lưới bóng chuyền...
- Vận dụng 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt trước của một công trình xây...
- Thực hành 2 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các tứ giác ở Hình 9, tứ...
- Vận dụng 3 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát Hình 10, cho biết...
- 2. Hình thoiThực hành 3 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi MNPQ có...
- Vận dụng 4 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ dài cạnh của các khuy áo...
- Vận dụng 5 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một hoa văn trang trí được ghép bởi...
- Vận dụng 6 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một tứ giác có chu vi là 52 cm và...
- Bài tậpBài tập 1 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cần thêm một điều kiện gì để...
- Bài tập 2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD, kẻ AH vuông...
- Bài tập 3 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi E là...
- Bài tập 4 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD (AB...
- Bài tập 5 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD. Gọi I,...
- Bài tập 6 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình 21. Chứng minh rằng tứ...
- Bài tập 7 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thoi ABCD, hai đường...
- Bài tập 8 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC cân tại A, gọi...
- Bài tập 9 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm các hình bình hành và hình thang...
- Khởi động trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát hình chụp các mái nhà...
- Khám phá 1 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 1a là hình ảnh của một...
- Khám phá 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có các cạnh...
- Khám phá 4 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 11a là hình chụp tấm lưới...
- Khám phá 5 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Hình thoi có là hình bình...
- Khám phá 6 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho ABCD là một hình bình...






{"content1": "Trường hợp 1: Vì AB = CD và AD = BC nên tứ giác ABCD là hình bình hành. Do đó, hai cặp cạnh đối của hình bình hành sẽ song song với nhau, từ đó suy ra AB // CD và AD // BC.","content2": "Trường hợp 2: Vì AB // CD và AB = CD nên tứ giác ABCD là hình chữ nhật. Trong hình chữ nhật, hai cặp cạnh kề sẽ có tỉ lệ bằng nhau, nên suy ra AB // CD và AD // BC.","content3": "Trường hợp 3: Vì AD // BC và AD = BC nên tứ giác ABCD là hình thoi. Trong hình thoi, cặp đường chéo sẽ vuông góc và cắt nhau tại trọng tâm của hình, từ đó suy ra AB // CD và AD // BC.","content4": "Trường hợp 4: Vì $\widehat{A}=\widehat{C},\widehat{B}=\widehat{D}$ nên tứ giác ABCD là hình bình thường (hình tứ giác có cả 4 góc bằng nhau). Trong hình bình thường, các cặp đường chéo sẽ cắt nhau ta trọng điểm, nên suy ra AB // CD và AD // BC.","content5": "Trường hợp 5: Vì PA = PC, PB = PD nên tứ giác APCD là hình vuông. Trong hình vuông, cặp cạnh đối sẽ cùng vuông góc với nhau và có cùng độ dài, từ đó suy ra AB // CD và AD // BC."}