Bài tập 2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD, kẻ AH vuông...
Câu hỏi:
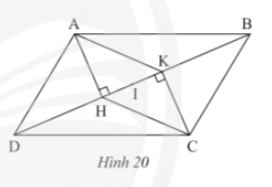
Bài tập 2 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 21)
a) Chứng minh tứ giác AHCK là hình bình hành
b) Gọi I là trung điểm của HK. Chứng minh IB = ID
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ánh
a) Phương pháp giải:- Xét tam giác vuông DKC và BHA:+ DC = AB (do là các cạnh của hình bình hành ABCD)+ $\widehat{CDK} = \widehat{ABH}$ (do AB//DC trong hình bình hành ABCD)Do đó, ta có $\Delta DKC = \Delta BHA$ (cùng chứng minh)- Vì AH $\perp$ BD và CK $\perp$ BD, nên ta có CK//AH- Xét tứ giác AKCH:Ta đã chứng minh được CK//AH, và CK = AHDo đó, ta suy ra tứ giác AKCH là hình bình hành (dấu hiệu 3)b) Phương pháp giải:- Vì AKCH là hình bình hành nên AC và HK cắt nhau tại trung điểm của mỗi đoạn.- Từ đó, suy ra I là trung điểm của AC và BDVậy nên IB = ID.Đáp án:a) Tứ giác AHCK là hình bình hànhb) IB = ID.
Câu hỏi liên quan:
- 1. Hình bình hànhThực hành 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình...
- Vận dụng 1 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mắt lưới của một lưới bóng chuyền...
- Vận dụng 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt trước của một công trình xây...
- Thực hành 2 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trong các tứ giác ở Hình 9, tứ...
- Vận dụng 3 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát Hình 10, cho biết...
- 2. Hình thoiThực hành 3 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thoi MNPQ có...
- Vận dụng 4 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính độ dài cạnh của các khuy áo...
- Vận dụng 5 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một hoa văn trang trí được ghép bởi...
- Vận dụng 6 trang 79 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một tứ giác có chu vi là 52 cm và...
- Bài tậpBài tập 1 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cần thêm một điều kiện gì để...
- Bài tập 3 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình bình hành ABCD. Gọi E là...
- Bài tập 4 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD (AB...
- Bài tập 5 trang 80 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình bình hành ABCD. Gọi I,...
- Bài tập 6 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình 21. Chứng minh rằng tứ...
- Bài tập 7 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thoi ABCD, hai đường...
- Bài tập 8 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC cân tại A, gọi...
- Bài tập 9 trang 81 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm các hình bình hành và hình thang...
- Khởi động trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Quan sát hình chụp các mái nhà...
- Khám phá 1 trang 73 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 1a là hình ảnh của một...
- Khám phá 2 trang 74 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có các cạnh...
- Khám phá 3 trang 75 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tứ giác ABCD có P là giao...
- Khám phá 4 trang 76 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình 11a là hình chụp tấm lưới...
- Khám phá 5 trang 77 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Hình thoi có là hình bình...
- Khám phá 6 trang 78 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho ABCD là một hình bình...






b) Gọi E là giao điểm của BC và AD. Ta có hai tam giác AHK và DKE đều vuông tại H và K. Do đó, I là trung điểm của DE và BC. Từ đó suy ra IB = ID. Vậy điều cần chứng minh đã được thể hiện.
b) Ta có I là trung điểm của HK nên IB = IH và ID = IK. Như vậy, ta có IB = IH = ID = IK. Vậy điều cần chứng minh được xác định.
a) Ta có AH // CK và AH = CK. Đồng thời, AH vuông góc với BD và CK vuông góc với BD. Vậy tứ giác AHCK là hình bình hành.
a) Gọi O là giao điểm của AC và BD. Ta có AHO và COK là hai tam giác vuông cân tại O. Do đó, ta có HO = OC và HA = CK. Vậy tứ giác AHCK là hình bình hành.
a) Ta có AH // CK do cả hai đều vuông góc với BD và cắt nhau tại K. Đồng thời, AH = CK do là đường cao của hình bình hành ABCD. Vậy tứ giác AHCK là hình bình hành.