Vận dụng 3 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đo chiều cao AB của một tòa...
Câu hỏi:
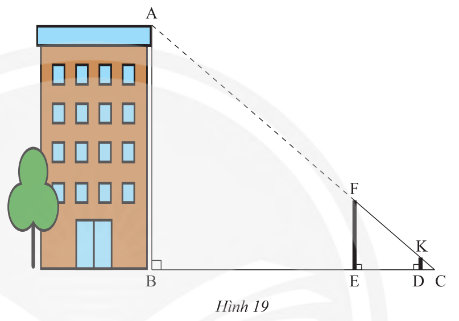
Vận dụng 3 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Đo chiều cao AB của một tòa nhà bằng hai cây cọc FE, DK, một sợi dây và một thước cuộn như sau:
- Đặt cọc FE cố định, di chuyển cọc DK sao cho nhìn thấy K, F, A thẳng hàng.
- Căng thẳng dây FC đi qua K và cắt mặt đất tại C.
- Đo khoảng cách BC và DC trên mặt đất
Cho biết DK = 1 m, BC = 24 m, DC = 1.2 m. Tính chiều cao AB của tòa nhà
Câu trả lời:
Người trả lời: GV. Đỗ Thị Vương
Phương pháp giải:Bước 1: Kẻ tam giác ABC với AB là chiều cao cần tìm, BC và AC là cạnh của tam giác ABC.Bước 2: Kẻ đường thẳng DK // AB và cắt BC tại point E.Bước 3: Ta có $\frac{AB}{DK}=\frac{BC}{DC}$ (theo định lí Thales).Bước 4: Thay vào phương trình ta có $\frac{AB}{1}=\frac{24}{1.2}$.Bước 5: Giải phương trình ta được $AB=20$.Vậy chiều cao AB của tòa nhà là 20m. Bạn cũng có thể giải bằng cách:- Sử dụng định lý Pythagoras để tính chiều cao AB: $AB^2 = BC^2 - DC^2 = 24^2 - 1.2^2 = 576 - 1.44 = 574.56$, từ đó $AB = \sqrt{574.56} \approx 23.99$.- Sử dụng định lý vuông góc cân để tính chiều cao AB: $DK = AB$ và $BC = \sqrt{24^2 - 1.2^2} = \sqrt{574.56}$, từ đó $AB = BC \approx 23.99$.
Câu hỏi liên quan:
- Hoạt động khởi động trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Những sợi cáp treo...
- 1. Đoạn thẳng tỉ lệHoạt động khám phá 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTSTa)...
- Thực hành 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính tỉ số của hai đoạn thẳng...
- Hoạt động khám phá 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: So ánh tỉ số của hai đoạn...
- Thực hành 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong hình 3, chứng minh rằng:a)...
- Vận dụng 1 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tìm các đoạn thẳng tỉ lệ trong...
- 2. Định lí Thales trong tam giácHoạt động khám phá 3 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Thực hành 3 trang 46 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x, y trong Hình 8
- Hoạt động khám phá 4 trang 47 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
- Thực hành 4 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài x trên Hình 13.
- Vận dụng 2 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu đo đạc được ghi trên...
- Hoạt động khám phá 5 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
- Thực hành 5 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy chỉ ra các cặp đường thẳng...
- Bài tậpBài tập 1 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Hãy đo chiều dài và...
- Bài tập 2 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm x trong Hình 20
- Bài tập 3 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu được ghi trên HÌnh 21....
- Bài tập 4 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 22, chứng minh rằng MN...
- Bài tập 5 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính các độ dài x, y trong Hình 23
- Bài tập 6 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 24, chỉ ra các cặp...
- Bài tập 7 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)...
- Bài tập 8 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)....
- Bài tập 9 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 25 và chứng minh...






Khi hai đỉnh A, K nằm trên một đường thẳng với cọc FE, ta áp dụng hệ thức Euclid: AB/BC = DK/DC. Thay số vào ta có AB/24 = 1/1.2, từ đó suy ra AB = 20m. Vậy chiều cao của tòa nhà là 20m.
Từ điều kiện đã cho, ta có AB/24 = 1/1.2 => AB = 24 * 1/1.2 = 20 m. Do đó, chiều cao của tòa nhà là 20m.
Theo định lý Ta-lét, ta có tỉ số giữa chiều cao và khoảng cách trên mặt đất của tòa nhà là bằng tỉ số giữa chiều cao và khoảng cách của cột DK. Vì vậy, ta có tỉ số AB/BC = DK/DC