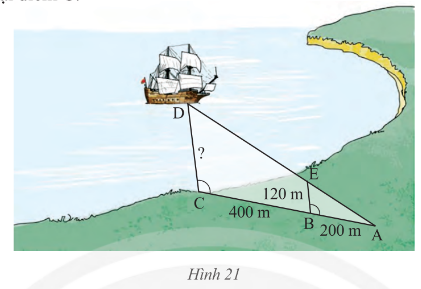
Bài tập 3 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu được ghi trên HÌnh 21....

Để tính khoảng cách CD, ta có thể sử dụng phương pháp tính toán trực tiếp dựa trên thông tin đã cho trong hình vẽ. Theo hình vẽ, ta thấy AB = 40m, BC = 30m. Khoảng cách CD chính là cạnh của hình chữ nhật ABCD, tức là CD = AB - BC = 40 - 30 = 10m.

Ta cũng có thể tính khoảng cách CD bằng cách sử dụng hệ thức tổ hợp trong hình học. Theo hình vẽ, ta thấy tam giác ABC là tam giác vuông tại C. Do đó, ta có thể sử dụng định lí Pytago để tính CD. Áp dụng công thức CD^2 = AB^2 - BC^2 = 40^2 - 30^2 = 1600 - 900 = 700, suy ra CD = √700 ≈ 26.46m.

Để tính khoảng cách CD từ con*** đến trạm quan tắc đặt tại điểm C, ta có thể sử dụng định lí Pytago trong tam giác vuông. Theo hình vẽ, ta có AB = 40m, BC = 30m. Áp dụng công thức c^2 = a^2 + b^2, ta tính được CD = √(AB^2 - BC^2) = √(40^2 - 30^2) = √(1600 - 900) = √700 ≈ 26.46m.