Hoạt động khám phá 5 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
Câu hỏi:
Hoạt động khám phá 5 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB = 6cm, AC = 15 cm. Trên AB, AC lần lượt lấy B', C' sao cho AB' = 2 cm, AC' = 5 cm
a) Tính các tỉ số $\frac{AB'}{AB}$ và $\frac{AC'}{AC}$
b) Qua B' vẽ đường thẳng song song với BC cắt AC tại E. Tính AE
c) So sánh AE và AC'
d) Hãy nhận xét về vị trí của E và C', vị trí của hai đường thẳng B'C' và B'E
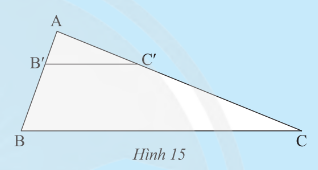
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Đức
a) Phương pháp giải 1:Ta có AB' = 2cm, AB = 6cm => $\frac{AB'}{AB}=\frac{2}{6}=\frac{1}{3}$Ta có AC' = 5cm, AC = 15cm => $\frac{AC'}{AC}=\frac{5}{15}=\frac{1}{3}$Phương pháp giải 2:Ta có AB' = 2cm, AB = 6cm => $\frac{AB'}{AB}=\frac{2}{6}=\frac{1}{3}$Ta có AC' = 5cm, AC = 15cm => $\frac{AC'}{AC}=\frac{5}{15}=\frac{1}{3}$b)Gọi E là giao điểm của B'E và AC.Ta có B'E // BC (theo đề bài).Theo định lí Thales, ta có $\frac{AB'}{AB}=\frac{AE}{AC}$.Suất ra $\frac{1}{3}=\frac{AE}{15}$, từ đó suy ra AE = 5cm.c)Ta đã có AE = 5cm, và AC' = 5cm => AE = AC'.d)Vì E thuộc AC và E là điểm cắt giữa AC và B'E nên E = C'.Vì E = C', nên B'C' và B'E cũng trùng nhau.Vậy câu trả lời đầy đủ và chi tiết hơn như sau:a) $\frac{AB'}{AB}=\frac{1}{3}$ và $\frac{AC'}{AC}=\frac{1}{3}$b) AE = 5cmc) AE = AC' = 5cmd) E = C' và B'C' = B'E.
Câu hỏi liên quan:
- Hoạt động khởi động trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Những sợi cáp treo...
- 1. Đoạn thẳng tỉ lệHoạt động khám phá 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTSTa)...
- Thực hành 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính tỉ số của hai đoạn thẳng...
- Hoạt động khám phá 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: So ánh tỉ số của hai đoạn...
- Thực hành 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong hình 3, chứng minh rằng:a)...
- Vận dụng 1 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tìm các đoạn thẳng tỉ lệ trong...
- 2. Định lí Thales trong tam giácHoạt động khám phá 3 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Thực hành 3 trang 46 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x, y trong Hình 8
- Hoạt động khám phá 4 trang 47 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
- Thực hành 4 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài x trên Hình 13.
- Vận dụng 2 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu đo đạc được ghi trên...
- Thực hành 5 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy chỉ ra các cặp đường thẳng...
- Vận dụng 3 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đo chiều cao AB của một tòa...
- Bài tậpBài tập 1 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Hãy đo chiều dài và...
- Bài tập 2 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm x trong Hình 20
- Bài tập 3 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu được ghi trên HÌnh 21....
- Bài tập 4 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 22, chứng minh rằng MN...
- Bài tập 5 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính các độ dài x, y trong Hình 23
- Bài tập 6 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 24, chỉ ra các cặp...
- Bài tập 7 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)...
- Bài tập 8 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)....
- Bài tập 9 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 25 và chứng minh...






d) Nhận xét về vị trí của E và C', vị trí của hai đường thẳng B'C' và B'E: Nếu B'E // BC và AE = $ rac{2}{7}AC$ thì vị trí của E và C' sẽ luôn thay đổi tùy vào giá trị của AC. Đường thẳng B'C' và B'E sẽ không cắt nhau vì chúng song song.
c) So sánh AE và AC': $AE = rac{2}{7}AC$ nên vị trí của E so với C' sẽ phụ thuộc vào giá trị của AC. Nếu AC lớn, E sẽ nằm xa hơn so với C'. Nếu AC nhỏ, E sẽ gần với C'.
b) Vì B'E // BC nên ta có $ rac{AE}{EC} = rac{AB'}{BC'} = rac{AB'}{AC'} = rac{2}{5}$. Từ đây suy ra $AE = rac{2}{7}AC$. Để tính được giá trị cụ thể của AE cần biết giá trị cạnh AC.
a) Tính các tỉ số: $ rac{AB'}{AB} = rac{2}{6} = rac{1}{3}$ và $ rac{AC'}{AC} = rac{5}{15} = rac{1}{3}$