2. Định lí Thales trong tam giácHoạt động khám phá 3 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2...
Câu hỏi:
2. Định lí Thales trong tam giác
Hoạt động khám phá 3 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trên một tờ giấy kẻ caro có các đường kẻ ngang song song và cách đều nhau.
a) Vẽ một đường thẳng d cắt các đường kẻ ngang của tờ giấy như trong Hình 5a. Hãy so sánh độ dài các đoạn thẳng MN, NP, PQ và QE
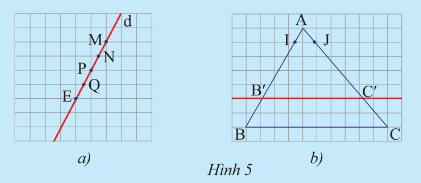
b) Vẽ một tam giác ABC rồi vẽ một đường thẳng song song với cạnh BC và cắt hai cạnh AB, AC lần lượt tại B' và C'. Trên cạnh AB, lấy đoạn AI làm đơn vị đo tính tỉ số AB' và B'B; trên cạnh AC, lấy đoạn AJ làm đơn vị đo tính tỉ số AC' và C'C (Hình 5b)
So sánh các tỉ số $\frac{AB'}{AB}$ và $\frac{AC'}{AC};\frac{AB'}{B'B}$ và $\frac{AC'}{C'C};\frac{B'B}{AB}$ và $\frac{C'C}{AC}$
Câu trả lời:
Người trả lời: GV. Đỗ Văn Dung
Để giải câu hỏi trên, ta sẽ sử dụng Định lí Thales trong tam giác.a) Để so sánh độ dài các đoạn thẳng MN, NP, PQ và QE, ta nhận thấy các đoạn thẳng đều nằm trên các đường kẻ ngang song song và cách đều nhau trên tờ giấy caro. Do đó, các đoạn thẳng MN, NP, PQ và QE có cùng độ dài.b) Để so sánh các tỉ số $\frac{AB'}{AB}$ và $\frac{AC'}{AC}$, ta thực hiện các bước sau:- Vẽ đường thẳng song song với cạnh BC và cắt hai cạnh AB, AC tại B' và C'.- Trên cạnh AB, lấy đoạn AI làm đơn vị đo, tính tỉ số $\frac{AB'}{AB}$ bằng $\frac{5AI}{7AI} = \frac{5}{7}$.- Tương tự, trên cạnh AC, lấy đoạn AJ làm đơn vị đo, tính tỉ số $\frac{AC'}{AC}$ bằng $\frac{5AJ}{7AJ} = \frac{5}{7}$.- Do $AB' || AC'$, ta có $\frac{AB'}{AB} = \frac{AC'}{AC}$.Để so sánh các tỉ số $\frac{AB'}{B'B}$ và $\frac{AC'}{C'C}$, ta tính tỉ số như sau:- $\frac{AB'}{B'B} = \frac{5AI}{2AI} = \frac{5}{2}$.- $\frac{AC'}{C'C} = \frac{5AJ}{2AJ} = \frac{5}{2}$.- Do $BB' || CC'$, ta có $\frac{AB'}{B'B} = \frac{AC'}{C'C}$.Cuối cùng, để so sánh các tỉ số $\frac{B'B}{AB}$ và $\frac{C'C}{AC}$, ta tính tỉ số như sau:- $\frac{B'B}{AB} = \frac{2AI}{7AI} = \frac{2}{7}$.- $\frac{C'C}{AC} = \frac{2AJ}{7AJ} = \frac{2}{7}$.- Vậy, ta có $\frac{B'B}{AB} = \frac{C'C}{AC} = \frac{2}{7}$. Như vậy, sau khi thực hiện phương pháp giải trên, ta có thể đi đến kết luận chính xác và chi tiết như trên.
Câu hỏi liên quan:
- Hoạt động khởi động trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Những sợi cáp treo...
- 1. Đoạn thẳng tỉ lệHoạt động khám phá 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTSTa)...
- Thực hành 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính tỉ số của hai đoạn thẳng...
- Hoạt động khám phá 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: So ánh tỉ số của hai đoạn...
- Thực hành 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong hình 3, chứng minh rằng:a)...
- Vận dụng 1 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tìm các đoạn thẳng tỉ lệ trong...
- Thực hành 3 trang 46 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x, y trong Hình 8
- Hoạt động khám phá 4 trang 47 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
- Thực hành 4 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài x trên Hình 13.
- Vận dụng 2 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu đo đạc được ghi trên...
- Hoạt động khám phá 5 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
- Thực hành 5 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy chỉ ra các cặp đường thẳng...
- Vận dụng 3 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đo chiều cao AB của một tòa...
- Bài tậpBài tập 1 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Hãy đo chiều dài và...
- Bài tập 2 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm x trong Hình 20
- Bài tập 3 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu được ghi trên HÌnh 21....
- Bài tập 4 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 22, chứng minh rằng MN...
- Bài tập 5 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính các độ dài x, y trong Hình 23
- Bài tập 6 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 24, chỉ ra các cặp...
- Bài tập 7 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)...
- Bài tập 8 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)....
- Bài tập 9 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 25 và chứng minh...






Để so sánh độ dài các đoạn thẳng và tỉ số giữa chúng, ta có thể áp dụng tỉ lệ song song. Khi có các đường thẳng song song cắt qua một tam giác, chúng tạo ra các đoạn thẳng tương tự với tỉ lệ nhất định. Việc so sánh tỉ lệ giữa các đoạn thẳng giúp chúng ta hiểu rõ hơn về mối quan hệ giữa các phần tử trong tam giác và trong hình vẽ.
Để so sánh các tỉ số $ rac{AB'}{AB}$ và $ rac{AC'}{AC}; rac{AB'}{B'B}$ và $ rac{AC'}{C'C}; rac{B'B}{AB}$ và $ rac{C'C}{AC}$, ta cần tính độ dài các đoạn thẳng và sử dụng công thức tính tỉ số. Bằng cách so sánh các tỉ số này, ta có thể xác định được mối quan hệ giữa các phần tử trong tam giác ABC và tam giác tạo ra bởi việc vẽ đường thẳng song song.
Để so sánh độ dài các đoạn thẳng MN, NP, PQ và QE, ta có thể áp dụng định lí Thales trong tam giác. Theo định lí Thales, khi có hai đường thẳng song song cắt qua một tam giác, các đoạn thẳng tương ứng trên các cạnh song song đó có tỉ lệ bằng nhau. Vậy ta có thể so sánh các đoạn thẳng bằng cách tính tỉ lệ giữa chúng.