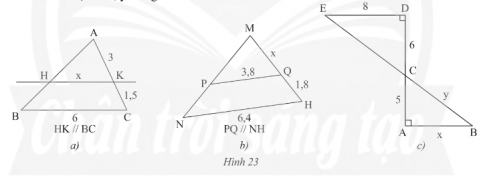
Bài tập 5 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính các độ dài x, y trong Hình 23

Để giải bài toán trên, chúng ta có thể thực hiện theo các phương pháp sau:

Phương pháp 1:
- Xét tam giác ABC có HK // BC. Theo định lí Thales, ta có: $\frac{HK}{BC}=\frac{AK}{AC}$
- Suy ra: $\frac{x}{6}=\frac{3}{3+1.5}$
- Giải phương trình trên ta được: $x = 4$

Phương pháp 2:
- Xét tam giác MNH có PQ // NH. Theo định lí Thales, ta có: $\frac{MQ}{MH}=\frac{PQ}{NH}$
- Suy ra: $\frac{x}{x+1.8}=\frac{3.8}{6.4}$
- Giải phương trình trên ta được: $x = \frac{171}{65}$

Phương pháp 3:
- Ta có DE // AB (cùng vuông góc với AD). Theo định lí Thales, ta có: $\frac{CD}{CA}=\frac{CE}{CB}=\frac{DE}{AB}$
- Suy ra: $\frac{6}{5}=\frac{\sqrt{8^{2}+6^{2}}}{y}=\frac{8}{x}$
- Giải hệ phương trình trên ta được: $x = \frac{20}{3}$ và $y = \frac{25}{3}$

Vậy, câu trả lời đầy đủ và chi tiết cho câu hỏi trên là:
a) $x = 4$
b) $x = \frac{171}{65}$
c) $x = \frac{20}{3}$ và $y = \frac{25}{3}$