Hoạt động khám phá 4 trang 47 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
Câu hỏi:
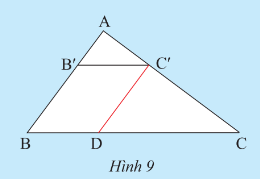
Hoạt động khám phá 4 trang 47 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB = 6cm, AC = 8 cm và BC = 10 cm. Lấy điểm B' trên AB sao cho AB' = 2 cm. Qua B' vẽ đường thẳng sóng song với BC và cắt AC tại C'.
a) Tính AC'
b) Qua C' vẽ đường thẳng song song với AB và cắt BC tại D. Tính BD, B'C'
c) Tính và so sánh các tỉ số: $\frac{AB'}{AB},\frac{AC'}{AC}$ và $\frac{B'C'}{BC}$
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Long
Phương pháp giải:a) Từ điều kiện B'C' // BC, ta áp dụng định lí Thales trong tam giác ABC để tính được AC':$\frac{AB'}{AB}=\frac{AC'}{AC}$$\frac{2}{6}=\frac{AC'}{8}$AC' = $\frac{8}{3}$b) Từ điều kiện C'D // AB, ta áp dụng định lí Thales trong tam giác ABC để tính được BD:$\frac{BD}{BC}=\frac{AC'}{AC}$$\frac{BD}{10}=\frac{\frac{8}{3}}{8}$$BD = \frac{10}{3}$Từ đó, suy ra B'C' = BD = $\frac{10}{3}$c) So sánh tỉ số:$\frac{AB'}{AB}=\frac{2}{6}=\frac{1}{3}$$\frac{AC'}{AC}=\frac{\frac{8}{3}}{8}=\frac{1}{3}$$\frac{B'C'}{BC}=\frac{\frac{10}{3}}{10}=\frac{1}{3}$Vậy có $\frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}= \frac{1}{3}$Vậy câu trả lời đầy đủ và chi tiết hơn cho câu hỏi trên là:a) AC' = $\frac{8}{3}$b) BD = $\frac{10}{3}$, B'C' = $\frac{10}{3}$c) $\frac{AB'}{AB}=\frac{AC'}{AC}=\frac{B'C'}{BC}=\frac{1}{3}$
Câu hỏi liên quan:
- Hoạt động khởi động trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Những sợi cáp treo...
- 1. Đoạn thẳng tỉ lệHoạt động khám phá 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTSTa)...
- Thực hành 1 trang 44 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tính tỉ số của hai đoạn thẳng...
- Hoạt động khám phá 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: So ánh tỉ số của hai đoạn...
- Thực hành 2 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong hình 3, chứng minh rằng:a)...
- Vận dụng 1 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy tìm các đoạn thẳng tỉ lệ trong...
- 2. Định lí Thales trong tam giácHoạt động khám phá 3 trang 45 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Thực hành 3 trang 46 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính độ dài x, y trong Hình 8
- Thực hành 4 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm độ dài x trên Hình 13.
- Vận dụng 2 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu đo đạc được ghi trên...
- Hoạt động khám phá 5 trang 48 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ABC có AB =...
- Thực hành 5 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Hãy chỉ ra các cặp đường thẳng...
- Vận dụng 3 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đo chiều cao AB của một tòa...
- Bài tậpBài tập 1 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Hãy đo chiều dài và...
- Bài tập 2 trang 49 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm x trong Hình 20
- Bài tập 3 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Với số liệu được ghi trên HÌnh 21....
- Bài tập 4 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 22, chứng minh rằng MN...
- Bài tập 5 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tính các độ dài x, y trong Hình 23
- Bài tập 6 trang 50 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 24, chỉ ra các cặp...
- Bài tập 7 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)...
- Bài tập 8 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Cho hình thang ABCD (AB // CD)....
- Bài tập 9 trang 51 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 25 và chứng minh...






c) Ta có 3 tỉ số: $ rac{AB'}{AB} = rac{2}{6} = rac{1}{3}$, $ rac{AC'}{AC} = 1$ và $ rac{B'C'}{BC} = rac{6}{10} = rac{3}{5}$. So sánh ta được $ rac{AB'}{AB} < rac{AC'}{AC} < rac{B'C'}{BC}$.
b) Ta có BD = CD = 4 cm và B'C' = 6 cm.
a) Ta có AC' = AC = 8 cm.