Vận dụng 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tứ giác EFGH có các góc cho như...
Câu hỏi:
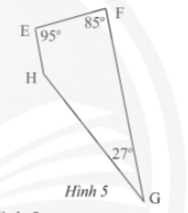
Vận dụng 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tứ giác EFGH có các góc cho như Hình 5
a) Chứng minh rằng EFGH là hình thang
b) Tìm góc chưa biết của tứ giác
Câu trả lời:
Người trả lời: GV. Đỗ Thị Việt
a) Phương pháp giải:Ta có $\widehat{E} + \widehat{F} = 95^\circ + 85^\circ = 180^\circ$, tức là $\widehat{E}$ và $\widehat{F}$ là hai góc bù nhau và chúng lại ở vị trí trong cùng phía. Ta suy ra $EH \parallel FG$, do đó tứ giác $EFGH$ là hình thang.b) Phương pháp giải:Hình thang $EFGH$ có hai góc đối diện nhau bằng nhau, nên $\widehat{H} = 180^\circ - \widehat{G} = 180^\circ - 27^\circ = 153^\circ$.Vậy câu trả lời là:a) Tứ giác $EFGH$ là hình thang.b) Góc chưa biết của tứ giác $EFGH$ là $\widehat{H} = 153^\circ$.
Câu hỏi liên quan:
- 1.Hình thang - Hình thang cânThực hành 1 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Vận dụng 1 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một mặt tường của chân tháp cột cờ...
- 2. Tính chất của hình thang cânThực hành 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm...
- Vận dụng 3 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một khung cửa sổ hình thang cân có...
- 3. Dấu hiệu nhận biết hình thang cânThực hành 3 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Vận dụng 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt cắt của một li giấy đựng bỏng...
- Bài tậpBài tập 1 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: TÌm x và y ở các hình sau.
- Bài tập 2 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD có AB = CD, BD là...
- Bài tập 3 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác nhọn ABC có AH là...
- Bài tập 4 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC vuông tại A...
- Bài tập 5 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tứ giác nào trong Hình 15 là...
- Bài tập 6 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thang ABCD có AB // CD. Qua...
- Bài tập 7 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt bên của một chiếc vali (Hình...
- Khởi động trang 68 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Mái ngói của trụ sở Ủy ban nhân...
- Khám phá 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tứ giác ABCD (Hình 1b) là hình...
- Khám phá 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Cho hình thang cân ABCD có...
- Khám phá 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thang ABCD có hai đáy...






Kết quả cuối cùng: Góc chưa biết của tứ giác EFGH là x = 90 độ. Vậy tứ giác EFGH là hình thang và góc chưa biết là 90 độ.
Gọi góc chưa biết trong tứ giác EFGH là x. Tổng các góc trong tứ giác là: x + x + 90 + 90 = 360 độ. Giải phương trình này, ta sẽ tìm được giá trị của góc chưa biết x.
Để tính góc chưa biết của tứ giác EFGH, ta có thể áp dụng tổng các góc trong một tứ giác bằng 360 độ. Từ đó, ta có thể tính được góc chưa biết của tứ giác.
Xét tứ giác EFGH, ta có EF // HG (do góc EFG = góc HGF, có trong sách giáo khoa trang 69). Tương tự, ta có FG // EH (do góc FGH = góc EHG, cũng có trong sách giáo khoa trang 69). Vậy EFGH là hình thang.
Để chứng minh rằng tứ giác EFGH là hình thang, ta cần chứng minh hai cặp đường đối nhau của tứ giác EFGH là song song. Ta có thể sử dụng tính chất của các góc trong hình để chứng minh điều này.