Khám phá 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Cho hình thang cân ABCD có...
Câu hỏi:
Khám phá 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:
a) Cho hình thang cân ABCD có hai đáy là AB và CD (AB > CD). Qua C vẽ đường thẳng song song với AD và cắt AB tại E (Hình 6a).
i) Tam giác CEB là tam giác gì? Vì sao?
ii) So sánh AD và BC.
b) Cho hình thang cân MNPQ có hai đáy là MN và PQ (Hỉnh 6b). So sánh MP và NQ. Giải thích.
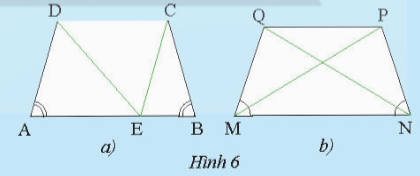
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Ánh
a) i) Tam giác CEB là tam giác cân tại C vì hai góc ở đỉnh CEB và BCE bằng nhau (cùng bằng $\widehat{E}$). ii) Ta có AD = CE (cùng bằng nhau vì đều bằng đáy hình thang cân) và CE = BC (vì CE // AD và cắt AB tại E) nên ta kết luận rằng AD = BC.b) Ta biết MQ = NP (vì cùng là đáy hình thang cân) và góc QMN = góc PNM (vì cùng là góc trong). Khi đó, điểm NQ = MP.
Câu hỏi liên quan:
- 1.Hình thang - Hình thang cânThực hành 1 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Vận dụng 1 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một mặt tường của chân tháp cột cờ...
- Vận dụng 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tứ giác EFGH có các góc cho như...
- 2. Tính chất của hình thang cânThực hành 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm...
- Vận dụng 3 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một khung cửa sổ hình thang cân có...
- 3. Dấu hiệu nhận biết hình thang cânThực hành 3 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Vận dụng 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt cắt của một li giấy đựng bỏng...
- Bài tậpBài tập 1 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: TÌm x và y ở các hình sau.
- Bài tập 2 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD có AB = CD, BD là...
- Bài tập 3 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác nhọn ABC có AH là...
- Bài tập 4 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC vuông tại A...
- Bài tập 5 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tứ giác nào trong Hình 15 là...
- Bài tập 6 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thang ABCD có AB // CD. Qua...
- Bài tập 7 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt bên của một chiếc vali (Hình...
- Khởi động trang 68 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Mái ngói của trụ sở Ủy ban nhân...
- Khám phá 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tứ giác ABCD (Hình 1b) là hình...
- Khám phá 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thang ABCD có hai đáy...






Ta có MN = PQ (vì hình thang cân) và MP = NQ (vì là đường chéo của hình thang). Từ đó suy ra MP = NQ = MN = PQ.
Do MP và NQ là đường chéo của hình thang cân MNPQ, nên chúng có cùng độ dài. Đồng thời, MP sẽ cắt NQ tạo thành góc vuông nên MP = NQ.
MP và NQ là các đường chéo của hình thang cân MNPQ, chúng có cùng độ dài và đồng thời cắt nhau ở góc vuông. Vì vậy, ta có MP = NQ.
ii) Ta có BC = CE (do CE là chiều cao của hình thang cân ABCD) và AD = AB (vì hình thang cân). Do đó, ta có AD > BC.
i) Tam giác CEB là tam giác cân vì hai cạnh CE và CB có độ dài bằng nhau (do CE là cạnh của hình chữ nhật ACEB cùng với AB).