Bài tập 6 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thang ABCD có AB // CD. Qua...
Câu hỏi:
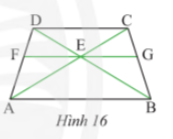
Bài tập 6 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hình thang ABCD có AB // CD. Qua giao điểm E của AC và BD, ta vẽ đường thẳng song song với AB cắt AD, BC lần lượt tại F và G (Hình 16). Chứng minh rằng EG là tia phân giác góc CEB.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Dung
Để chứng minh rằng EG là tia phân giác góc CEB, ta có thể giải bài toán theo phương pháp sau:Phương pháp giải:- Ta có tam giác ACD và BDC đều có 2 góc bằng nhau, từ đó suy ra $\widehat{ACD} = \widehat{BDC}$ và $\Delta ACD = \Delta BDC$.- Vì FG // CD nên ta có $\widehat{BEG} = \widehat{BDC}$ (đồng vị) và $\widehat{GEC} = \widehat{ACD}$.- Từ đó, suy ra $\widehat{BEG} = \widehat{GEC}$ hay EG là tia phân giác góc CEB.Vậy EG là tia phân giác góc CEB.Câu trả lời: EG là tia phân giác góc CEB.
Câu hỏi liên quan:
- 1.Hình thang - Hình thang cânThực hành 1 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Vận dụng 1 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một mặt tường của chân tháp cột cờ...
- Vận dụng 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tứ giác EFGH có các góc cho như...
- 2. Tính chất của hình thang cânThực hành 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm...
- Vận dụng 3 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Một khung cửa sổ hình thang cân có...
- 3. Dấu hiệu nhận biết hình thang cânThực hành 3 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1...
- Vận dụng 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt cắt của một li giấy đựng bỏng...
- Bài tậpBài tập 1 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: TÌm x và y ở các hình sau.
- Bài tập 2 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho tứ giác ABCD có AB = CD, BD là...
- Bài tập 3 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác nhọn ABC có AH là...
- Bài tập 4 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho tam giác ABC vuông tại A...
- Bài tập 5 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tứ giác nào trong Hình 15 là...
- Bài tập 7 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Mặt bên của một chiếc vali (Hình...
- Khởi động trang 68 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Mái ngói của trụ sở Ủy ban nhân...
- Khám phá 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tứ giác ABCD (Hình 1b) là hình...
- Khám phá 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Cho hình thang cân ABCD có...
- Khám phá 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Cho hình thang ABCD có hai đáy...






Khi vẽ đường thẳng EG, ta có EF // AB và BG // DC. Từ đó, suy ra hai tam giác AEF và BGC đồng dạng theo định lý điểm chung trong tam giác. Do đó, ta có CEB = CEG, tức là EG là tia phân giác góc CEB.
Gọi I là giao điểm của EG và CB. Ta có AB // CD nên tam giác AEF và tam giác FDC đồng dạng, suy ra EF/FC = AE/CD. Tương tự, ta có BG/GD = BD/AD. Kết hợp hai phương trình trên, ta được EF/FC = BG/GD. Do đó, ta có EG là tia phân giác góc CEB.
Ta có AB // CD và EF // AB nên tam giác AEF và tam giác FDC đồng dạng. Do đó, ta có AE/AF = CD/CF. Tương tự, ta cũng có BD/BG = AD/DG. Kết hợp hai phương trình trên, suy ra AE/AF = BG/DG. Do đó, ta có EG là tia phân giác góc CEB.