CHƯƠNG I: MỆNH ĐỀ VÀ TẬP HỢP
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 1 Mệnh đề.
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Tập hợp.
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 3 Các phép toán trên tập hợp
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương I
CHƯƠNG II: BẤT PHƯƠNG TRÌNH VÀ HỆ BẤT PHƯƠNG TRÌNH BẬC NHẤT HAI ẨN
CHƯƠNG III: HÀM SỐ BẬC HAI VÀ ĐỒ THI
CHƯƠNG IV: HỆ THƯC LƯỢNG TRONG TAM GIÁC
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 1 Giá trị lượng giác của một góc từ 0 độ đến 180 độ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Định lí côsin và định lí sin
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 3 Giải bài tập tam giác và ứng dụng thực tế
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương IV
CHƯƠNG V: VECTO
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 1 Khái niệm vectơ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Tổng và hiệu của hai vectơ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 3 Tích của một số với một vectơ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 4 Tích vô hướng của hai vectơ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương V
CHƯƠNG VI: THỐNG KÊ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 1 Số gần đúng và sai số
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 2 Mô tả và biểu diễn dữ liệu trên các bảng và biểu đồ
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 3 Các số đặc trưng đo xu thế trung tâm của mẫu số liệu
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài 4 Các số đặc trưng đo mức độ phân tán của mẫu số liệu
- Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo bài Bài tập cuối chương VI
Giải bài tập sách bài tập (SBT) toán lớp 10 chân trời sáng tạo Bài bài tập cuối chương II
https://s.shopee.vn/AKN2JyAJAw
Hướng dẫn giải Bài bài tập cuối chương II trang 39 sách bài tập (SBT) toán lớp 10
Trong bài bài tập cuối chương II trang 39 sách bài tập (SBT) toán lớp 10, chúng ta sẽ cùng tìm hiểu cách giải một số bài toán phức tạp nhưng rất thú vị. Đây là cơ hội để học sinh áp dụng kiến thức đã học vào thực tế và rèn luyện kỹ năng giải quyết vấn đề logic.
Việc hướng dẫn giải bài tập chi tiết và cụ thể sẽ giúp học sinh hiểu rõ hơn vấn đề, từ đó nắm vững kiến thức và phương pháp giải quyết. Đừng ngần ngại khi gặp khó khăn, hãy thử sức và sẵn sàng học hỏi từ những sai sót để khắc phục và tiến bộ hơn.
Chúc các em may mắn và thành công trong việc giải bài tập này!
Bài tập và hướng dẫn giải
Bài 1 : Bạn Danh để dành được 900 nghìn đồng. Trong một đợt ủng hộ trẻ em mồ côi, bạn Danh đã lấy ra x tờ tiền loại 50 nghìn đồng, y tờ tiền loại 100 nghìn đồng để trao tặng. Một bất phương trình mô tả điều kiện ràng buộc đối với x, y là:
A. 50x + 100y ≤ 900;
B. 50x + 100y ≥ 900;
C. 100x + 50y ≤ 900;
D. x + y = 900.
Bài 2 : Trong các bất phương trình sau, bất phương trình nào không phải là bất phương trình bậc nhất hai ẩn?
A. 2x – 3y – 2022 ≤ 0;
B. 5x + y ≥ 2x + 11;
C. x + 2025 > 0;
D. xy+1>0">$\frac{1}{2}$+ xy+1>0">1 > 0.
Bài 3 : Miền không bị gạch chéo (không kể bờ d) trong Hình 1 là miền nghiệm của bất phương trình nào trong các bất phương trình dưới đây?
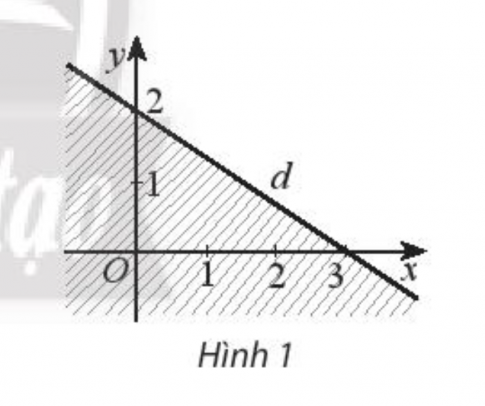
A. 2x + 3y < 6;
B. 2x + 3y > 6;
C. xy+1>0">$\frac{x}{2}$ + xy+1>0">$\frac{y}{3}$ > 0;
xy+1>0">D. xy+1>0">xy+1>0">$\frac{x}{2}$ + xy+1>0">$\frac{y}{3}$ < 1.
Bài 4 : Miền tam giác không gạch chéo trong Hình 2 là miền nghiệm của hệ bất phương trình nào trong các hệ bất phương trình dưới đây?
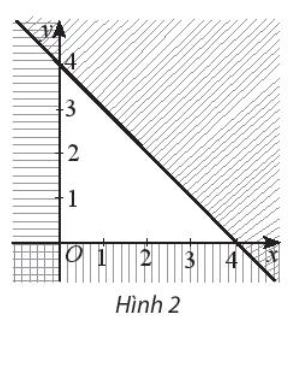
A. $\left\{\begin{matrix}x + y - 4 ≥ 0 & & \\ x ≤ 0 & & \\ y ≥ 0 & & \end{matrix}\right.$
B. $\left\{\begin{matrix}x + y - 4 ≥ 0 & & \\ x ≥ 0 & & \\ y ≤ 0 & & \end{matrix}\right.$
C. $\left\{\begin{matrix}x + y ≥ 4 & & \\ x ≥ 0 & & \\ y ≥ 0 & & \end{matrix}\right.$
D. $\left\{\begin{matrix}x + y - 4 ≥ 0 & & \\ x ≤ 0 & & \\ y ≤ 0 & & \end{matrix}\right.$
Bài 5 : Biểu thức F = 2x – 8y đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?
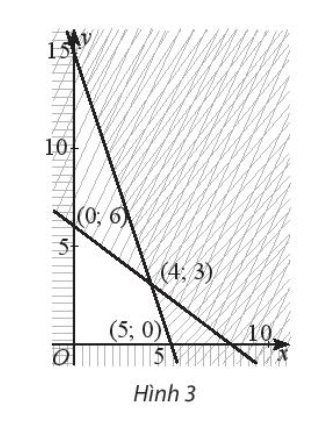
A. – 48;
B. 0;
C. – 160;
D. – 40.
Bài 6 : Biểu thức F = 5x + 2y đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?
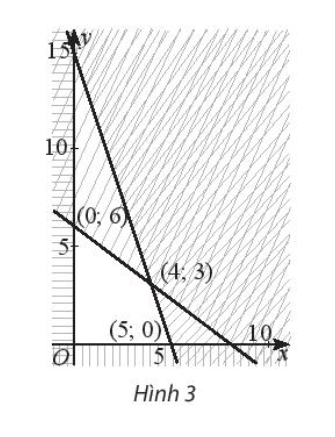
A. 30;
B. 12;
C. 25;
D. 26.
Bài 1 : Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong Hình 4 (mỗi ô vuông có cạnh là 1 đơn vị).
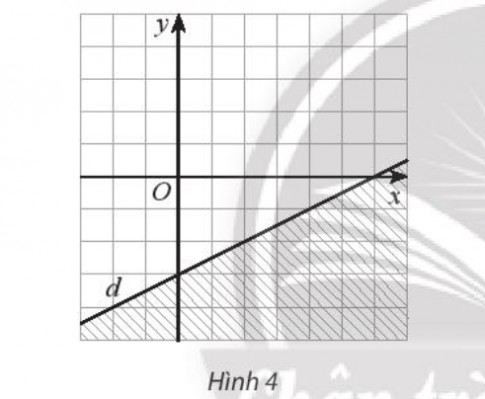
Bài 2 : Đường thẳng 4x + 3y = 12 và hai trục tọa độ chia mặt phẳng Oxy thành các miền như Hình 5. Hãy tìm hệ bất phương trình có miền nghiệm là miền B (kể cả bờ).
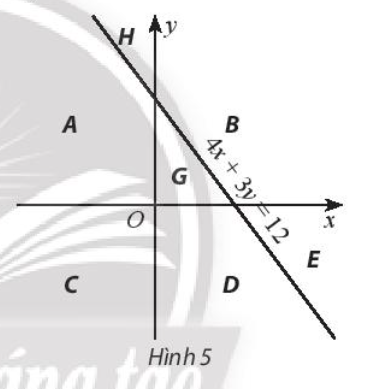
Bài 3 : Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây.
| x | 0 | 0 | 1 | 1 | 2 | 2 | 4 |
| y | 2 | 4 | 0 | 1 | 0 | 1 | 0 |
| F = 4x + 5y | |||||||
| G = 5x – 3y |
Trong các giá trị tìm được:
a) tìm GTLN của F.
b) tìm GTNN của G.
Bài 4 : Trên miền đa giác không gạch chéo ở Hình 6, hãy:
a) Tìm GTLN của F = 2x + 3y;
b) Tìm GTNN của G = x – 4y.
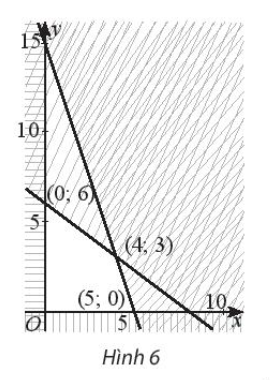
Bài 5 : Bác Dũng dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Bác chỉ có không quá 9 triệu đồng để mua hạt giống. Cho biết tiền mua hạt giống cà tím là 200 000 đồng/sào và cà chua là 100 000 đồng/sào. Viết hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y.
Bài 6 : Một phân xưởng lắp ráp máy tính dự định ráp x chiếc máy tính cá nhân và y chiếc máy tính bảng trong một ngày. Do hạn chế về nhân công nên mỗi ngày chỉ có thể xuất xưởng tổng hai loại máy tính trên không quá 150 chiếc. Viết hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y.
Bài 7 : Bạn Hoàng dự định mua x con cá vàng và y con cá Koi từ một trang trại cá giống. Cho biết mỗi con cá vàng có giá 35 nghìn đồng và mỗi con cá Koi có giá 150 nghìn đồng. Hoàng chỉ để dành được 1,7 triệu đồng và trại cá chỉ bán mỗi loại cá từ 10 con trở lên. Hãy viết hệ bất phương trình mô tả điều kiện ràng buộc đối với x, y.
Bài 8 : Một học sinh dự định làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ thiện. Cần 1 giờ để làm một bình hoa loại nhỏ và sẽ bán với giá 100 nghìn đồng, 90 phút để làm một bình hoa loại lớn và sẽ bán với giá 200 nghìn đồng. Học sinh này chỉ thu xếp được 15 giờ nghỉ để làm và ban tổ chức yêu cầu phải làm ít nhất là 12 bình hoa. Hãy cho biết bạn ấy cần làm bao nhiêu bình hoa mỗi loại để gây quỹ từ thiện được nhiều tiền nhất.
Bài 9 : Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại sản phẩm X, Y. Để sản xuất một tấn sản phẩm X cần dùng 6 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 10 triệu đồng. Để sản xuất một tấn sản phẩm Y cần dùng 2 tấn nguyên liệu A và 2 tấn nguyên liệu B, khi bán lãi được 8 triệu đồng. Hãy lập kế hoạch sản xuất cho xưởng nói trên sao cho có tổng số tiền lãi cao nhất.
Giải bài tập sách giáo khoa (SGK) 10 Kết nối tri thức
- Soạn văn lớp 10 tập 1 kết nối tri thức
- Soạn văn lớp 10 tập 2 kết nối tri thức
- Văn mẫu lớp 10 kết nối tri thức
- Giải bài tập toán lớp 10 tập 1 kết nối tri thức
- Giải bài tập toán lớp 10 tập 2 kết nối tri thức
- Giải bài tập vật lí lớp 10 kết nối tri thức
- Giải bài tập hóa học lớp 10 kết nối tri thức
- Giải bài tập sinh học lớp 10 kết nối tri thức
- Giải bài tập Địa lí lớp 10 kết nối tri thức
- Giải bài tập lịch sử lớp 10 kết nối tri thức
- Giải bài tập tin học lớp 10 kết nối tri thức
- Giải bài tập Âm nhạc lớp 10 kết nối tri thức
- Giải bài tập mĩ thuật lớp 10 kết nối tri thức
- Giải bài tập giáo dục kinh tế pháp luật lớp 10 kết nối tri thức
- Giải bài tập giáo dục quốc phòng an ninh lớp 10 kết nối tri thức
- Giải bài tập hoạt động trải nghiệm lớp 10 kết nối tri thức
- Giải bài tập thiết kế công nghệ lớp 10 kết nối tri thức
- Giải bài tập công nghệ trồng trọt lớp 10 kết nối tri thức
- Giải bài tập giáo dục thể chất lớp 10 kết nối tri thức
- Giải bài tập tiếng anh lớp 10 Global Success
Giải bài tập sách giáo khoa (SGK) 10 Chân trời sáng tạo
- Soạn văn lớp 10 tập 1 chân trời sáng tạo
- Soạn văn lớp 10 tập 2 chân trời sáng tạo
- Văn mẫu lớp 10 chân trời sáng tạo
- Giải bài tập toán lớp 10 tập 1 chân trời sáng tạo
- Giải bài tập toán lớp 10 tập 2 chân trời sáng tạo
- Giải bài tập vật lí lớp 10 chân trời sáng tạo
- Giải bài tập hóa học lớp 10 chân trời sáng tạo
- Giải bài tập sinh học lớp 10 chân trời sáng tạo
- Giải bài tập Địa lí lớp 10 chân trời sáng tạo
- Giải bài tập lịch sử lớp 10 chân trời sáng tạo
- Giải bài tập tin học lớp 10 chân trời sáng tạo
- Giải bài tập Âm nhạc lớp 10 chân trời sáng tạo
- Giải bài tập mĩ thuật lớp 10 chân trời sáng tạo
- Giải bài tập giáo dục kinh tế pháp luật lớp 10 chân trời sáng tạo
- Giải bài tập Hoạt động trải nghiệm, hướng nghiệp lớp 10 chân trời sáng tạo bản 1
- Giải bài tập Hoạt động trải nghiệm, hướng nghiệp lớp 10 chân trời sáng tạo bản 2
- Giải bài tập giáo dục quốc phòng an ninh lớp 10 chân trời sáng tạo
- Giải bài tập thiết kế công nghệ lớp 10 chân trời sáng tạo
- Giải bài tập công nghệ trồng trọt lớp 10 chân trời sáng tạo
- Giải bài tập giáo dục thể chất lớp 10 chân trời sáng tạo
- Giải bài tập tiếng anh lớp 10 Friends Global
Giải bài tập sách giáo khoa (SGK) 10 Cánh diều
- Soạn văn lớp 10 tập 1 cánh diều
- Soạn văn lớp 10 tập 2 cánh diều
- Văn mẫu lớp 10 cánh diều
- Giải bài tập toán lớp 10 tập 1 cánh diều
- Giải bài tập toán lớp 10 tập 2 cánh diều
- Giải bài tập vật lí lớp 10 cánh diều
- Giải bài tập hóa học lớp 10 cánh diều
- Giải bài tập sinh học lớp 10 cánh diều
- Giải bài tập Địa lí lớp 10 cánh diều
- Giải bài tập lịch sử lớp 10 cánh diều
- Giải bài tập tin học lớp 10 cánh diều
- Giải bài tập Âm nhạc lớp 10 cánh diều
- Giải bài tập mĩ thuật lớp 10 cánh diều
- Giải bài tập giáo dục kinh tế pháp luật lớp 10 cánh diều
- Giải bài tập giáo dục quốc phòng an ninh lớp 10 cánh diều
- Giải bài tập hoạt động trải nghiệm lớp 10 cánh diều
- Giải bài tập thiết kế công nghệ lớp 10 cánh diều
- Giải bài tập công nghệ trồng trọt lớp 10 cánh diều
- Giải bài tập giáo dục thể chất lớp 10 cánh diều
- Giải bài tập tiếng anh lớp 10 Explore new worlds
Giải bài tập sách bài tập (SBT) lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 10 tập 1 kết nối tri thức
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 10 tập 2 kết nối tri thức
- Giải bài tập sách bài tập (SBT) toán lớp 10 tập 1 kết nối tri thức
- Giải bài tập sách bài tập (SBT) toán lớp 10 tập 2 kết nối tri thức
- Giải bài tập sách bài tập (SBT) hóa học lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) sinh học lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) vật lí lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) lịch sử lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) địa lí lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) tin học lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) giáo dục kinh tế pháp luật lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) giáo dục quốc phòng và an ninh lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm lớp 10 kết nối tri thức
- Giải bài tập sách bài tập (SBT) tiếng anh lớp 10 Global success
Giải bài tập sách bài tập (SBT) lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 10 tập 1 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 10 tập 2 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) toán lớp 10 tập 1 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) toán lớp 10 tập 2 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) hóa học lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) sinh học lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) vật lí lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) lịch sử lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) địa lí lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) giáo dục kinh tế pháp luật lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) giáo dục quốc phòng và an ninh lớp 10 chân trời sáng tạo
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm lớp 10 chân trời sáng tạo bản 1
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm lớp 10 chân trời sáng tạo bản 2
- Giải bài tập sách bài tập (SBT) tiếng anh lớp 10 Friends Global
Giải bài tập sách bài tập (SBT) lớp 10 Cánh diều
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 10 tập 1 cánh diều
- Giải bài tập sách bài tập (SBT) ngữ văn lớp 10 tập 2 cánh diều
- Giải bài tập sách bài tập (SBT) toán lớp 10 tập 1 cánh diều
- Giải bài tập sách bài tập (SBT) toán lớp 10 tập 2 cánh diều
- Giải bài tập sách bài tập (SBT) hóa học lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) sinh học lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) vật lí lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) lịch sử lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) địa lí lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) tin học lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) giáo dục kinh tế pháp luật lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) hoạt động trải nghiệm lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) giáo dục quốc phòng và an ninh lớp 10 cánh diều
- Giải bài tập sách bài tập (SBT) tiếng anh lớp 10 Explore new world
Giải bài tập chuyên đề học tập 10 Kết nối tri thức
- Giải bài tập chuyên đề toán lớp 10 kết nối tri thức
- Giải bài tập chuyên đề ngữ văn lớp 10 kết nối tri thức
- Giải bài tập chuyên đề vật lí lớp 10 kết nối tri thức
- Giải bài tập chuyên đề hóa học lớp 10 kết nối tri thức
- Giải bài tập chuyên đề sinh học lớp 10 kết nối tri thức
- Giải bài tập chuyên đề lịch sử lớp 10 kết nối tri thức
- Giải bài tập chuyên đề địa lí lớp 10 kết nối tri thức
- Giải bài tập chuyên đề công nghệ trồng trọt lớp 10 kết nối tri thức
- Giải bài tập chuyên đề giáo dục kinh tế và pháp luật lớp 10 kết nối tri thức
- Giải bài tập chuyên đề tin học lớp 10 theo định hướng tin học ứng dụng kết nối tri thức
- Giải bài tập chuyên đề tin học lớp 10 theo định hướng khoa học máy tính kết nối tri thức
- Giải bài tập chuyên đề mĩ thuật lớp 10 kết nối tri thức
Giải bài tập chuyên đề học tập 10 Chân trời sáng tạo
- Giải bài tập chuyên đề toán lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề ngữ văn lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề vật lí lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề hóa học lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề sinh học lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề địa lí lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề lịch sử lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề giáo dục kinh tế và pháp luật lớp 10 chân trời sáng tạo
- Giải bài tập chuyên đề âm nhạc lớp 10 chân trời sáng tạo
Giải bài tập chuyên đề học tập 10 Cánh diều
- Giải bài tập chuyên đề toán lớp 10 cánh diều
- Giải bài tập chuyên đề ngữ văn lớp 10 cánh diều
- Giải bài tập chuyên đề vật lí lớp 10 cánh diều
- Giải bài tập chuyên đề hóa học lớp 10 cánh diều
- Giải bài tập chuyên đề sinh học lớp 10 cánh diều
- Giải bài tập chuyên đề địa lí lớp 10 cánh diều
- Giải bài tập chuyên đề lịch sử lớp 10 cánh diều
- Giải bài tập chuyên đề công nghệ trồng trọt lớp 10 cánh diều
- Giải bài tập chuyên đề giáo dục kinh tế và pháp luật lớp 10 cánh diều
- Giải bài tập chuyên đề tin học lớp 10 theo định hướng tin học ứng dụng cánh diều
- Giải bài tập chuyên đề tin học lớp 10 theo định hướng khoa học máy tính cánh diều
- Giải bài tập chuyên đề âm nhạc lớp 10 cánh diều





