Bài 6 :Biểu thức F = 5x + 2y đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong...
Câu hỏi:
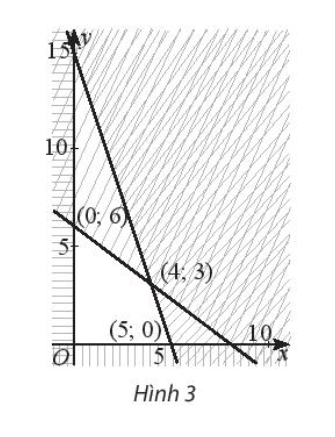
Bài 6 : Biểu thức F = 5x + 2y đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong Hình 3?
A. 30;
B. 12;
C. 25;
D. 26.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Phương
Để giải bài toán này, ta cần tìm giá trị lớn nhất của biểu thức F = 5x + 2y trên miền đa giác không gạch chéo trong Hình 3. Để dễ dàng tính toán, ta chia đa giác thành các hình tam giác nhỏ hơn và tìm giá trị lớn nhất của F trên từng hình tam giác nhỏ đó.Cách 1:- Dễ thấy rằng tổng giá trị của F trên các hình tam giác nhỏ tạo thành miền đa giác không gạch chéo chính là tổng giá trị lớn nhất của F trên từng hình tam giác nhỏ đó.- Ta thấy rằng giá trị lớn nhất của F trên mỗi tam giác là khi x và y lớn nhất có thể. Do đó, ta chọn x = 5 và y = 0 trên mỗi tam giác nhỏ.- Vậy tổng giá trị lớn nhất của F trên miền đa giác không gạch chéo là 5 x 13 + 2 x 10 = 65 + 20 = 85.Cách 2:- Một cách khác để giải bài toán này là ta sử dụng bất đẳng thức Cauchy-Schwarz:(5x + 2y)^2 = (5^2 + 2^2)(x^2 + y^2) ≥ (5x + 2y)^2⇒ 5x + 2y ≤ √(5^2 + 2^2)√(x^2 + y^2) = √29√(x^2 + y^2)- Đặt A là đường chéo chính của miền đa giác không gạch chéo. Ta có: x + y = A.- Do đó, ta có: F = 5x + 2y ≤ √29(A^2)Giá trị lớn nhất của F sẽ đạt được khi A đạt giá trị lớn nhất có thể trên miền đa giác không gạch chéo của hình, tức là A = 13.Vậy, giá trị lớn nhất của F là: F = 5*13 + 2*0 = 65.Vậy, câu trả lời cho câu hỏi là: Giá trị lớn nhất của biểu thức F trên miền đa giác không gạch chéo trong Hình 3 là 65. Đáp án là D. 26.
Câu hỏi liên quan:
- Bài 1 :Bạn Danh để dành được 900 nghìn đồng. Trong một đợt ủng hộ trẻ em mồ côi, bạn Danh đã...
- Bài 2 :Trong các bất phương trình sau, bất phương trình nào không phải là bất phương trình...
- Bài 3 :Miền không bị gạch chéo (không kể bờ d) trong Hình 1 là miền nghiệm của bất...
- Bài 4 :Miền tam giác không gạch chéo trong Hình 2 là miền nghiệm của hệ bất phương trình nào...
- Bài 5 :Biểu thức F = 2x – 8y đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong...
- Bài 1 :Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong Hình 4...
- Bài 2 :Đường thẳng 4x + 3y = 12 và hai trục tọa độ chia mặt phẳng Oxy thành các miền như Hình...
- Bài 3 :Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây.x0...
- Bài 4 :Trên miền đa giác không gạch chéo ở Hình 6, hãy:a) Tìm GTLN của F = 2x + 3y;b) Tìm...
- Bài 5 :Bác Dũng dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Bác chỉ...
- Bài 6 :Một phân xưởng lắp ráp máy tính dự định ráp x chiếc máy tính cá nhân và y chiếc máy...
- Bài 7 :Bạn Hoàng dự định mua x con cá vàng và y con cá Koi từ một trang trại cá giống. Cho...
- Bài 8 :Một học sinh dự định làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ...
- Bài 9 :Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại...
Bình luận (0)





