Bài 4 :Trên miền đa giác không gạch chéo ở Hình 6, hãy:a) Tìm GTLN của F = 2x + 3y;b) Tìm...
Câu hỏi:
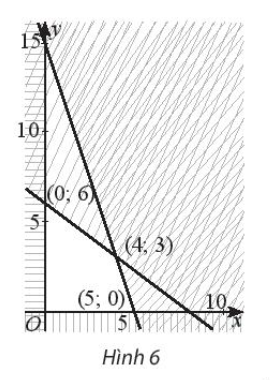
Bài 4 : Trên miền đa giác không gạch chéo ở Hình 6, hãy:
a) Tìm GTLN của F = 2x + 3y;
b) Tìm GTNN của G = x – 4y.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Giang
Phương pháp giải:Để tìm GTLN của F = 2x + 3y trên miền đa giác không gạch chéo, ta cần tính giá trị của hàm số F tại các đỉnh của đa giác và so sánh để tìm giá trị lớn nhất. Tương tự, để tìm GTNN của G = x - 4y trên miền đa giác không gạch chéo, ta cũng cần tính giá trị của hàm số G tại các đỉnh và so sánh để tìm giá trị nhỏ nhất.Câu trả lời chi tiết và đầy đủ:a) Tính giá trị của hàm số F = 2x + 3y tại các đỉnh của đa giác:F(0; 0) = 2(0) + 3(0) = 0F(0; 6) = 2(0) + 3(6) = 18F(4; 3) = 2(4) + 3(3) = 14F(5; 0) = 2(5) + 3(0) = 10Vì 0 < 10 < 14 < 18 nên giá trị lớn nhất của hàm số F là 18, tại đỉnh có tọa độ (0; 6).b) Tính giá trị của hàm số G = x - 4y tại các đỉnh của đa giác:G(0; 0) = 0 - 4(0) = 0G(0; 6) = 0 - 4(6) = -24G(4; 3) = 4 - 4(3) = -8G(5; 0) = 5 - 4(0) = 5Vì -24 < -8 < 0 < 5 nên giá trị nhỏ nhất của hàm số G là -24, tại đỉnh có tọa độ (0; 6).
Câu hỏi liên quan:
- Bài 1 :Bạn Danh để dành được 900 nghìn đồng. Trong một đợt ủng hộ trẻ em mồ côi, bạn Danh đã...
- Bài 2 :Trong các bất phương trình sau, bất phương trình nào không phải là bất phương trình...
- Bài 3 :Miền không bị gạch chéo (không kể bờ d) trong Hình 1 là miền nghiệm của bất...
- Bài 4 :Miền tam giác không gạch chéo trong Hình 2 là miền nghiệm của hệ bất phương trình nào...
- Bài 5 :Biểu thức F = 2x – 8y đạt GTNN bằng bao nhiêu trên miền đa giác không gạch chéo trong...
- Bài 6 :Biểu thức F = 5x + 2y đạt GTLN bằng bao nhiêu trên miền đa giác không gạch chéo trong...
- Bài 1 :Tìm bất phương trình có miền nghiệm là miền không gạch chéo (kể cả bờ d) trong Hình 4...
- Bài 2 :Đường thẳng 4x + 3y = 12 và hai trục tọa độ chia mặt phẳng Oxy thành các miền như Hình...
- Bài 3 :Tìm giá trị của F và G tương ứng với các giá trị x, y được cho trong bảng dưới đây.x0...
- Bài 5 :Bác Dũng dự định quy hoạch x sào đất trồng cà tím và y sào đất trồng cà chua. Bác chỉ...
- Bài 6 :Một phân xưởng lắp ráp máy tính dự định ráp x chiếc máy tính cá nhân và y chiếc máy...
- Bài 7 :Bạn Hoàng dự định mua x con cá vàng và y con cá Koi từ một trang trại cá giống. Cho...
- Bài 8 :Một học sinh dự định làm các bình hoa bằng giấy để bán trong một hội chợ gây quỹ từ...
- Bài 9 :Một xưởng sản xuất có 12 tấn nguyên liệu A và 8 tấn nguyên liệu B để sản xuất hai loại...
Bình luận (0)





