Bài tập 16. Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có...
Câu hỏi:
Bài tập 16. Một bộ thu năng lượng mặt trời để làm nóng nước được làm bằng một tấm thép không gỉ có mặt cắt hình parabol (Hình 2). Nước sẽ chảy thông qua một dường ống nằm ở tiêu điểm của parabol.
a. Viết phương trình chính tắc của parabol.
b. Tính khoảng cách từ tâm đường ống đến đỉnh của parabol.
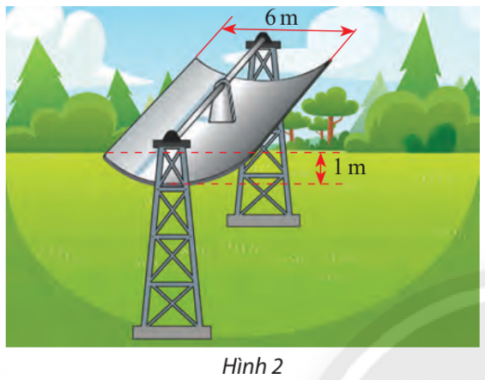
Câu trả lời:
Người trả lời: GV. Đỗ Thị Hạnh
a. Cách làm:Chọn hệ tọa độ như hình vẽ:Phương trình parabol (P) có dạng: y^2 = 2pxTa có: A(1; 3) thuộc (P) nên thay tọa độ điểm A vào phương trình (P), ta được:3^2 = 2p * 1⇒ p = 9/2Vậy phương trình chính tắc của parabol (P) là: y^2 = 9x.b. Cách làm:Vì đường ống nằm ở tiêu điểm của (P) nên khoảng cách từ tâm đường ống đến đỉnh của parabol bằng p/2 = 9/4 = 2.25 (m).Câu trả lời đầy đủ và chi tiết hơn là:a. Phương trình chính tắc của parabol là y^2 = 9x. b. Khoảng cách từ tâm đường ống đến đỉnh của parabol là 2.25 mét.
Câu hỏi liên quan:
- Bài tập 3.Tìm tọa độ giao điểm và góc giữa hai đường thẳng $d_{1}$ và $d_{2}$ trong mỗi...
- Bài tập 4.Tính bán kính của đường tròn tâm M(-2; 3) và tiếp xúc với đường thẳng:d: $14x...
- Bài tập 5. Tính khoảng cách giữa hai đường thẳng:$\Delta$: $6x + 8y - 13 = 0$$\Delta'$: $3x + 4y -...
- Bài tập 6. Tìm tâm và bán kính của các đường tròn có phương trình:a. $(x - 2)^{2} + (y - 7)^{2} =...
- Bài tập 7. Lập phương trình đường tròn trong các trường hợp sau:a. Có tâm I(-2; 4) và bán kính bằng...
- Bài tập 8. Viết phương trình tiếp tuyến của đường tròn (C): $(x - 5)^{2} + (y - 3)^{2}$ = 100 tại...
- Bài tập 9. Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục lớn và trục nhỏ của các elip...
- Bài tập 10. Viết phương trình chính tắc của elip thỏa mãn từng điều kiện:a. Đỉnh (5; 0), (0; 4);b....
- Bài tập 11. Tìm tọa độ các tiêu điểm, tọa độ các đỉnh, độ dài trục thực và trục ảo của các hypebol...
- Bài tập 12. Viết phương trình chính tắc của hypebol thảo mãn từng điều kiện sau:a. Đỉnh (3; 0),...
- Bài tập 13. Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:a. $y^{2} =...
- Bài tập 14. Viết phương trình chính tắc của parabol thảo mãn từng điều kiện sau:a. Tiêu điểm (4; ...
- Bài tập 15. Một gương lõm có mặt cắt hình parabol như Hình 1, có tiêu điểm cách đỉnh 5cm. Cho biết...
- Bài tập 17. Cổng chào của một thành phố có dạng hình parabol có khoảng cách giữa hai chân cổng là...
- Bài tập 18. Một người đứng ở giữa một tấm ván gỗ đặt trên một giàn giáo để sơn tường nhà. Biết rằng...






Các bước chi tiết để giải phương trình chính tắc của parabol và tính khoảng cách từ tâm đường ống đến đỉnh của parabol sẽ giúp bạn hiểu rõ vấn đề và có thể hoàn thành bài tập 16 một cách chính xác.
b. Khoảng cách từ tâm đường ống đến đỉnh của parabol sẽ là khoảng cách từ tâm đường ống đến tiêu điểm của parabol. Để tính khoảng cách này, ta sử dụng công thức khoảng cách giữa hai điểm trong hệ tọa độ. Đầu tiên, tìm tọa độ tiêu điểm và tọa độ tâm đường ống từ phương trình đã xác định. Sau đó, tính khoảng cách giữa chúng để có kết quả cuối cùng.
a. Phương trình chính tắc của parabol là y = ax^2 + bx + c, với (a, b, c) là hằng số cần xác định. Để tìm các hệ số này, ta cần biết 3 điểm trên parabol: đỉnh, điểm cực trị và điểm trên trục tung khi x = 0.