Giải bài tập 2 Hoán vị, chỉnh hợp và tổ hợp
Để giúp học sinh nắm vững kiến thức về hoán vị, chỉnh hợp và tổ hợp, sách "Giải bài tập 2: Hoán vị, chỉnh hợp và tổ hợp" là nguồn tư liệu hữu ích. Trong sách này, có phần đáp án chuẩn và hướng dẫn giải chi tiết cho từng bài tập trong chương trình học của sách giáo khoa. Hi vọng rằng, qua sách này, các em học sinh sẽ hiểu và nắm vững kiến thức bài học.
Khởi động
Trong phần này, sách đưa ra một ví dụ về việc chọn cầu thủ từ một đội bóng và sắp xếp chúng để thực hiện một loạt đá luân lưu. Bằng cách sử dụng quy tắc nhân, sách giải thích cách tính số cách chọn và sắp xếp cầu thủ một cách chi tiết và dễ hiểu.
Hoán vị
Sau đó, sách giải thích khái niệm hoán vị và cung cấp một vài ví dụ minh họa. Bằng cách lập các hoán vị, học sinh có thể hiểu rõ hơn về khái niệm này.
Chỉnh hợp
Qua ví dụ về việc chọn và cắm cờ trên một trạm quan sát, sách giải thích về chỉnh hợp và cung cấp các cách tính số cách chọn và cắm cờ một cách chi tiết.
Tổ hợp
Trong phần này, sách giải thích về tổ hợp thông qua việc chọn sách để đọc và sắp xếp chúng. Bằng cách cung cấp ví dụ và tính toán, sách giúp học sinh nắm vững kiến thức về tổ hợp.
Đồng thời, sách cũng cung cấp một số ví dụ và bài tập thực hành để học sinh có thể tự rèn luyện kỹ năng và nắm vững kiến thức. Qua việc áp dụng lý thuyết vào thực tiễn, học sinh sẽ hiểu sâu hơn về hoán vị, chỉnh hợp và tổ hợp.
Bài tập và hướng dẫn giải
Bài tập 1. Cần xếp một nhóm 5 học sinh ngồi vào một dãy 5 chiếc ghế.
a. Có bao nhiêu cách xếp?
b. Nếu bạn Nga (một thành viên trong nhóm) nhất định muốn ngồi vào chiếc ghế ngoài cùng bên trái, thì có bao nhiêu cách xếp?

Bài tập 2. Từ các chữ số sau đây, có thể lập được bao nhiêu số tự nhiên có bốn chữ số khác nhau?
a. 1; 2; 3; 4; 5; 6.
b. 0; 1; 2; 3; 4; 5
Bài tập 3. Tổ Một có 4 bạn nam và 5 bạn nữ. Có bao nhiêu cách cử 3 bạn của tổ làm trực nhật trong mỗi trường hợp sau?
a. 3 bạn được chọn bất kì
b. 3 bạn gồm 2 nam và 1 nữ.
Bài tập 4. Từ một danh sách gồm 8 người, người ta bầu ra một ủy ban gồm một chủ tịch, một phó chủ tịch, một thư kí và một ủy viên. Có bao nhiêu khả năng có thể về kết quả bầu ủy ban này?
Bài tập 5. Một nhóm gồm 7 bạn đến trung tâm chăm sóc người cao tuổi làm từ thiện. Theo chỉ dẫn của trung tâm, 3 bạn hỗ trợ đi lại, 2 bạn hỗ trợ tắm rửa và 2 bạn hỗ trợ ăn uống. Có bao nhiêu cách phân công các bạn trong nhóm làm các công việc trên?
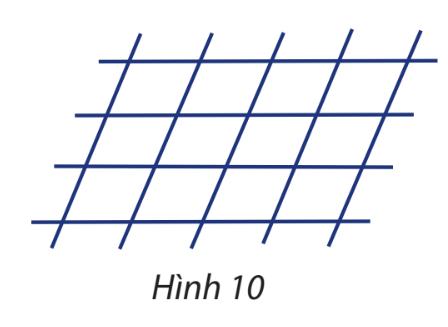
Bài tập 6. Có 4 đường thẳng song song cắt 5 đường thẳng song song khác tạo thành những hình bình hành (như Hình 10). Có bao nhiêu hình bình hành được tạo thành?
Bài tập 7. Mùa giải 2019, giải bóng đá vô địch quốc gia (V.League) có 14 đội bóng tham giá. Các đội bóng đấu vòng tròn hai lượt đi và về. Hỏi cả giải đấu có bao nhiêu trận đấu?





