Thực hành 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 12.a) Chứng minh...
Câu hỏi:
Thực hành 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 12.
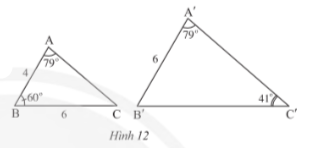
a) Chứng minh rằng $\Delta ABCᔕ\Delta A'B'C'$
b) Tính độ dài B'C'
Câu trả lời:
Người trả lời: GV. Đỗ Thị Giang
Phương pháp giải:a) Ta có:- $\angle C = 180^{\circ} - (\angle A + \angle B) = 41^{\circ}$- Xét tam giác ABC và tam giác A'B'C', ta có: $\angle A = \angle A' = 79^{\circ}$ $\angle C = \angle C' = 41^{\circ}$Do đó, ta có $\Delta ABC \cong \Delta A'B'C'$ (theo trường hợp góc - góc).b) Vì $\Delta ABC \cong \Delta A'B'C'$, nên ta có tỉ số đồng dạng:$\frac{AB}{A'B'} = \frac{BC}{B'C'}$Ta có $\frac{4}{6} = \frac{6}{B'C'}$Suy ra $B'C' = 9$Vậy, độ dài $B'C'$ là 9.
Câu hỏi liên quan:
- Hoạt động khởi động trang 67 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Các trường hợp đồng dạng...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT (c.c.c)Hoạt động khám phá 1 trang 67 sách giáo khoa (SGK) toán lớp...
- Thực hành 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm trong Hình 4 các cặp tam giác...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI (c.g.c)Hoạt động khám phá 2 trang 68 sách giáo khoa (SGK) toán lớp...
- Thực hành 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ADE và tam giác ACF...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA (g.g)Hoạt động khám phá 3 trang 69 sách giáo khoa (SGK) toán lớp 8...
- Vận dụng 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB // CD) có...
- Vận dụng 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Qua các trường hợp đồng dạng của...
- BÀI TẬPTrường hợp đồng dạng thứ nhất (c.c.c)Bài tập 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập...
- Bài tập 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tam giác ABC có độ dài AB = 4 cm, AC...
- Bài tập 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Một công viên có hai đường chạy...
- Trường hợp đồng dạng thứ hai (c.g.c)Bài tập 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 5 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 17, cho biết DE = 6 cm,...
- Bài tập 6 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Cho tam giác ABC có AB = 12...
- Trường hợp đồng dạng thứ ba (g.g)Bài tập 7 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 8 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 20a, cho biết...
- Bài tập 9 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 21a, cho biết...
- Bài tập 10 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đường đi và khoảng cách từ nhà...






{"Trả lời 1": Chứng minh rằng $\Delta ABC $ và $\Delta A'B'C'$ đồng dạng bằng cách chứng minh tỉ số các độ dài đồng quan hệ: $ \frac{AB}{A'B'} = \frac{BC}{B'C'} = \frac{AC}{A'C'} $."Trả lời 2": Để chứng minh $\Delta ABC $ và $\Delta A'B'C'$ đồng dạng, ta cần chứng minh 2 góc trong các tam giác tương đương nhau. "Trả lời 3": Sử dụng định lý hệ số góc: Nếu 2 tam giác có 2 góc đồng quy tương ứng bằng nhau thì 2 tam giác đó đồng dạng."Trả lời 4": Áp dụng định lý Sin trong tam giác để tìm được các tỉ số giữa các cạnh: $ \frac{AB}{sin\angle A} = \frac{AC}{sin\angle B} = \frac{BC}{sin\angle C} $"Trả lời 5": Sử dụng thuật giải đồng dạng để chứng minh $\Delta ABC $ và $\Delta A'B'C'$ với các điều kiện tương tự."Trả lời 6": Khảo sát và so sánh các góc và cạnh tương ứng trong hai tam giác để kết luận chúng đồng dạng. }