1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI (c.g.c)Hoạt động khám phá 2 trang 68 sách giáo khoa (SGK) toán lớp...
Câu hỏi:
1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI (c.g.c)
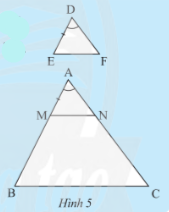
Hoạt động khám phá 2 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác DEF và ABC có $DE=\frac{1}{3}AB, DF=\frac{1}{3}AC,\widehat{D}=\widehat{A}$ (Hình 5). Trên tia AB, lấy điểm M sao cho AM = DE. Qua M kẻ MN // BC ($N\in AC$)
a) So sánh các tỉ số $\frac{AM}{AB}$ và $\frac{AN}{AC}$
b) So sánh AN và DF
c) Tam giác AMN có đồng dạng với tam giacsc ABC không?
d) Dự đoán sự đồng dạng của hai tam giác DEF và ABC
Câu trả lời:
Người trả lời: GV. Đỗ Văn Phương
a) Phương pháp giải:- Ta có $AM = DE = \frac{1}{3}AB$ và $AN = AC - AM = AC - \frac{1}{3}AB$.- Vậy $\frac{AM}{AB} = \frac{1}{3}$ và $\frac{AN}{AC} = \frac{AC - \frac{1}{3}AB}{AC} = 1 - \frac{1}{3} = \frac{2}{3}$.- Do đó, $\frac{AM}{AB} < \frac{AN}{AC}$.b) Phương pháp giải:- Ta đã có $AN = AC - \frac{1}{3}AB$ và $DF = \frac{1}{3}AC$.- Vì $AC > AB$, nên $AC - \frac{1}{3}AB > \frac{1}{3}AC$.- Do đó, $AN > DF$.c) Phương pháp giải:- Vì MN // BC nên ta có $\frac{AM}{AB} = \frac{AN}{AC}$.- Vậy tam giác AMN đồng dạng với tam giác ABC theo định lí Ta - lét.d) Phương pháp giải:- Ta đã có $\widehat{D} = \widehat{A}$, $DE = AM$ và $DF = AN$.- Vậy tam giác DEF đồng dạng với tam giác AMN theo quy tắc bất đẳng thức cạnh và góc.Câu trả lời đầy đủ:a) Ta có $\frac{AM}{AB} < \frac{AN}{AC}$.b) Ta có $AN > DF$.c) Tam giác AMN đồng dạng với tam giác ABC.d) Dự đoán đúng, tam giác DEF đồng dạng với tam giác ABC.
Câu hỏi liên quan:
- Hoạt động khởi động trang 67 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Các trường hợp đồng dạng...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT (c.c.c)Hoạt động khám phá 1 trang 67 sách giáo khoa (SGK) toán lớp...
- Thực hành 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm trong Hình 4 các cặp tam giác...
- Thực hành 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ADE và tam giác ACF...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA (g.g)Hoạt động khám phá 3 trang 69 sách giáo khoa (SGK) toán lớp 8...
- Thực hành 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 12.a) Chứng minh...
- Vận dụng 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB // CD) có...
- Vận dụng 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Qua các trường hợp đồng dạng của...
- BÀI TẬPTrường hợp đồng dạng thứ nhất (c.c.c)Bài tập 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập...
- Bài tập 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tam giác ABC có độ dài AB = 4 cm, AC...
- Bài tập 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Một công viên có hai đường chạy...
- Trường hợp đồng dạng thứ hai (c.g.c)Bài tập 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 5 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 17, cho biết DE = 6 cm,...
- Bài tập 6 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Cho tam giác ABC có AB = 12...
- Trường hợp đồng dạng thứ ba (g.g)Bài tập 7 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 8 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 20a, cho biết...
- Bài tập 9 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 21a, cho biết...
- Bài tập 10 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đường đi và khoảng cách từ nhà...






f) Từ AMN và ABC, ta nhận thấy MN // BC và AN = MN = $ rac{1}{3}$AC, nên ta có $ rac{AM}{AB} = rac{1}{3} = rac{AN}{AC}$, từ đó suy ra tam giác AMN đồng dạng với tam giác ABC.
e) Vì tam giác DEF và tam giác ABC có tỉ số cạnh tương ứng bằng nhau, nên chúng đồng dạng với nhau.
d) Dựa vào thông tin đã cho, ta có $DE = rac{1}{3}AB$ và $DF = rac{1}{3}AC$. Vậy ta dự đoán tam giác DEF đồng dạng với tam giác ABC theo nguyên tắc tỉ lệ 1:3.
c) Tam giác AMN và tam giác ABC không đồng dạng vì chúng có các cạnh tương ứng không tỉ lệ với nhau (AM không tương ứng với AB).
b) Ta có $AN = rac{1}{3}AC$ và $DF = rac{1}{3}AC$ nên $AN = DF$.