Bài tập 5 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 17, cho biết DE = 6 cm,...
Câu hỏi:
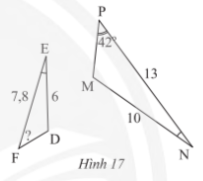
Bài tập 5 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 17, cho biết DE = 6 cm, EF= 7,8 cm, NP = 13 cm, NM = 10 cm, $\widehat{E}=\widehat{N}$ và $\widehat{P}=42^{\circ}$. Tính $\widehat{F}$
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ánh
Để giải bài toán này, ta sử dụng định lý cạnh - góc - cạnh cho hai tam giác:
Ta có:
$\frac{DE}{MN}=\frac{EF}{NP}=\frac{6}{10}=\frac{3}{5}$
Và $\widehat{E}=\widehat{N}$
Vậy ta có $\Delta DEF \sim \Delta MNP$ (theo nhận thức về tam giác đồng dạng).
Do đó, ta có $\widehat{F}=\widehat{P}=42^{\circ}$.
Vậy kết quả là: $\widehat{F}=42^{\circ}$.
Ta có:
$\frac{DE}{MN}=\frac{EF}{NP}=\frac{6}{10}=\frac{3}{5}$
Và $\widehat{E}=\widehat{N}$
Vậy ta có $\Delta DEF \sim \Delta MNP$ (theo nhận thức về tam giác đồng dạng).
Do đó, ta có $\widehat{F}=\widehat{P}=42^{\circ}$.
Vậy kết quả là: $\widehat{F}=42^{\circ}$.
Câu hỏi liên quan:
- Hoạt động khởi động trang 67 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Các trường hợp đồng dạng...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT (c.c.c)Hoạt động khám phá 1 trang 67 sách giáo khoa (SGK) toán lớp...
- Thực hành 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm trong Hình 4 các cặp tam giác...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI (c.g.c)Hoạt động khám phá 2 trang 68 sách giáo khoa (SGK) toán lớp...
- Thực hành 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ADE và tam giác ACF...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA (g.g)Hoạt động khám phá 3 trang 69 sách giáo khoa (SGK) toán lớp 8...
- Thực hành 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 12.a) Chứng minh...
- Vận dụng 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB // CD) có...
- Vận dụng 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Qua các trường hợp đồng dạng của...
- BÀI TẬPTrường hợp đồng dạng thứ nhất (c.c.c)Bài tập 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập...
- Bài tập 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tam giác ABC có độ dài AB = 4 cm, AC...
- Bài tập 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Một công viên có hai đường chạy...
- Trường hợp đồng dạng thứ hai (c.g.c)Bài tập 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 6 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Cho tam giác ABC có AB = 12...
- Trường hợp đồng dạng thứ ba (g.g)Bài tập 7 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 8 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 20a, cho biết...
- Bài tập 9 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 21a, cho biết...
- Bài tập 10 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đường đi và khoảng cách từ nhà...






{
"content1": "Ta có: EF = EN + NF = 7,8 cm. Với tam giác ENF vuông tại E, ta áp dụng định lý cosin ta được công thức: cos(E) = NF/EF. Từ đó suy ra NF = EF * cos(E) = 7,8 * cos(42) ≈ 5,46 cm.",
"content2": "Xét tam giác ENF ta có: NF/EF = cos(E) => NF/7,8 = cos(42) => NF ≈ 5,46 cm. Vì NF = NM - MF => MF = NM - NF = 10 - 5,46 ≈ 4,54 cm.",
"content3": "Từ EF = EN + NF => 7,8 = 6 + NF => NF = 7,8 - 6 ≈ 1,8 cm. Vì NF = NM - MF => MF = NM - NF = 10 - 1,8 ≈ 8,2 cm.",
"content4": "Ta có: MF = NM - NF = 10 - NP*sin(P) = 10 - 13*sin(42) ≈ 4,01 cm. Do đó $\widehat{F}$ = arctan(MF/EF) = arctan(4,01 / 7,8) ≈ 27,45 độ.",
"content5": "Do EF = EN + NF => 7,8 = 6 + NF => NF = 1,8 cm. Vì NF = NP*sin(42) => NP = NF/sin(42) = 1,8/sin(42) ≈ 2,7 cm. Tương tự, MF = NM - NP*cos(P) = 10 - 13*cos(42) ≈ 2,53 cm.",
"content6": "Ta có: EF = EN + NF => 7,8 = 6 + NF => NF = 1,8 cm. Vì NF = NP*sin(42) => NP = NF/sin(42) = 1,8/sin(42) ≈ 2,7 cm. Vì MF = NP*cos(P) = 13*cos(42) ≈ 9,65 cm. Từ đó suy ra $\widehat{F}$ = arccos(MF/EF) = arccos(9,65 / 7,8) ≈ 36,31 độ."
}