Thực hành 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ADE và tam giác ACF...
Câu hỏi:
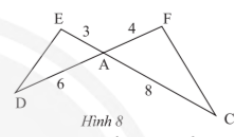
Thực hành 2 trang 69 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho tam giác ADE và tam giác ACF có các kích thước như trong Hình 8. Chứng minh rằng $\Delta ADEᔕ\Delta ACF$
Câu trả lời:
Người trả lời: GV. Đỗ Văn Dung
Để chứng minh rằng tam giác ADE đồng dạng với tam giác ACF, ta cần chứng minh hai điều kiện sau:1. $\frac{AE}{AF}=\frac{AD}{AC}$2. $\widehat{DAE}=\widehat{CAF}$Phương pháp giải:Ta có:$\frac{AE}{AF}=\frac{3}{4}$$\frac{AD}{AC}=\frac{6}{8}=\frac{3}{4}$Suy ra:$\frac{AE}{AF}=\frac{AD}{AC}$Hai góc đối đỉnh của hai tam giác cũng bằng nhau:$\widehat{DAE}=\widehat{CAF}$Vậy theo điều kiện đồng dạng tam giác (c.g.c), ta có: $\Delta ADEᔕ\Delta ACF$.Như vậy, tam giác ADE đồng dạng với tam giác ACF.
Câu hỏi liên quan:
- Hoạt động khởi động trang 67 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Các trường hợp đồng dạng...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ NHẤT (c.c.c)Hoạt động khám phá 1 trang 67 sách giáo khoa (SGK) toán lớp...
- Thực hành 1 trang 68 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tìm trong Hình 4 các cặp tam giác...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ HAI (c.g.c)Hoạt động khám phá 2 trang 68 sách giáo khoa (SGK) toán lớp...
- 1. TRƯỜNG HỢP ĐỒNG DẠNG THỨ BA (g.g)Hoạt động khám phá 3 trang 69 sách giáo khoa (SGK) toán lớp 8...
- Thực hành 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Quan sát Hình 12.a) Chứng minh...
- Vận dụng 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Cho hình thang ABCD (AB // CD) có...
- Vận dụng 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Qua các trường hợp đồng dạng của...
- BÀI TẬPTrường hợp đồng dạng thứ nhất (c.c.c)Bài tập 1 trang 70 sách giáo khoa (SGK) toán lớp 8 tập...
- Bài tập 2 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Tam giác ABC có độ dài AB = 4 cm, AC...
- Bài tập 3 trang 70 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Một công viên có hai đường chạy...
- Trường hợp đồng dạng thứ hai (c.g.c)Bài tập 4 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 5 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST: Trong Hình 17, cho biết DE = 6 cm,...
- Bài tập 6 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Cho tam giác ABC có AB = 12...
- Trường hợp đồng dạng thứ ba (g.g)Bài tập 7 trang 71 sách giáo khoa (SGK) toán lớp 8 tập 2...
- Bài tập 8 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 20a, cho biết...
- Bài tập 9 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:a) Trong Hình 21a, cho biết...
- Bài tập 10 trang 72 sách giáo khoa (SGK) toán lớp 8 tập 2 CTST:Đường đi và khoảng cách từ nhà...






Vậy tam giác ADE ᔕ tam giác ACF.
Do đó, ta đã chứng minh rằng tam giác ADE đồng dạng với tam giác ACF dựa trên nguyên lý góc tương ứng bằng nhau.
Cuối cùng, ta có góc EAD bằng góc FAC do chúng là góc ngoại tiếp khi các cạnh AD và AC song song.
Góc AED cũng bằng góc AFC vì chúng là góc đối của nhau khi hai góc tưng quyết đỉnh E và F.
Xét hai tam giác ADE và ACF, ta có góc ADE bằng góc ACF vì cả hai đều là góc nhọn với cùng đỉnh A.