Câu 6: Trang 49 sách VNEN 9 tập 1Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a >...
Câu hỏi:
Câu 6: Trang 49 sách VNEN 9 tập 1
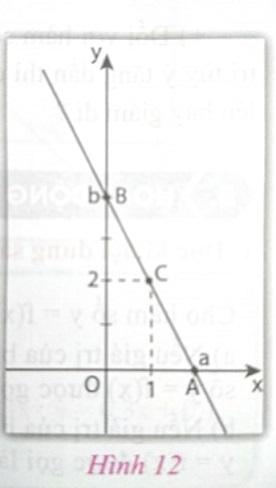
Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a > 0, b > 0) và C(1; 2) như trên hình 12.
a) Viết phương trình đường thẳng đi qua hai điểm A, B
b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.
c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Đức
a) Để viết phương trình đường thẳng đi qua hai điểm A(a; 0) và B(0; b), ta cần tìm được hệ số góc và hệ số tụ đề của đường thẳng. Gọi phương trình đường thẳng là (d): y = mx + n. Với đã cho, ta có n = b và m = $\frac{-b}{a}$. Vậy phương trình đường thẳng đi qua hai điểm A, B là (d): y = $\frac{-b}{a}$x + b.b) Để ba điểm A, B, C thẳng hàng, điểm C cần nằm trên đường thẳng đi qua A và B. Tức là C $\in $ (d). Thay tọa độ của C vào phương trình đường thẳng (d) ta có: 2 = $\frac{-b}{a} \cdot 1$ + b $\Rightarrow$ b = $\frac{2a}{a - 1}$c) Tiếp tục từ phần b, để ba điểm A, B, C thẳng hàng, ta cần giải phương trình b = $\frac{2a}{a - 1}$ để tìm ra giá trị của a và b. Sau đó, tính diện tích tam giác OAB và tìm giá trị của a để diện tích tam giác OAB nhỏ nhất. Áp dụng phương pháp đạo hàm, ta có a = 2, b = 4 để diện tích tam giác OAB đạt giá trị nhỏ nhất.Vậy kết quả là a = 2, b = 4 để ba điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất là 4.
Câu hỏi liên quan:
- C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 48 sách VNEN 9 tập 1Đồ thị của hàm số y =$\frac{2}{5}$x -...
- Câu 2: Trang 48 sách VNEN 9 tập 1Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song...
- Câu 3: Trang 48 sách VNEN 9 tập 1Tìm tọa độ giao điểm của đồ thị các đồ thị hàm số:a) y = 5x - 7 và...
- Câu 4: Trang 48 sách VNEN 9 tập 1Cho hàm số y =$\frac{1}{4}$x + 9. Viết công thức của các hàm...
- Câu 5: Trang 48 sách VNEN 9 tập 1Cho đường thẳng (d) y = ax + b. Tìm các giá trị của a, b trong mỗi...
- Câu 6: Trang 49 sách VNEN 9 tập 1Cho các đường thẳng(d1): y = x + 1 ; ...
- D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 1: Trang 49 sách VNEN 9 tập 1Hãy tự kiểm chứng mệnh...
- Câu 2: Trang 49 sách VNEN 9 tập 1Tính diện tích tam giác giới hạn bởi các đường y = x; y = -...
- Câu 3: Trang 49 sách VNEN 9 tập 1Trên mặt phẳng tọa độ Oxy cho hai điểm A(1; 1) và C(-1 ; -1).a)...
- Câu 4: Trang 49 sách VNEN 9 tập 1a) Viết phương trình các đường thẳng biết rằng các đường thẳng...
- Câu 5: Trang 49 sách VNEN 9 tập 1Viết phương trình đường thẳng đi qua A(4; 0) cắt tia Oy tại B(0;...






Vậy hệ thức liên hệ giữa a, b để ba điểm A, B, C thẳng hàng là b = 2a và để diện tích tam giác OAB nhỏ nhất thì a = 1 và b = 2.
Như vậy, phương trình đường thẳng đi qua A, B sẽ là y = 2x + 2.
c) Để tam giác OAB có diện tích nhỏ nhất thì ba điểm A, B, C phải thẳng hàng và diện tích tam giác OAB sẽ nhỏ nhất khi ta có a = 1 và b = 2.
b) Hệ thức liên hệ giữa a, b để ba điểm A, B, C thẳng hàng là b = 2a.
a) Phương trình đường thẳng đi qua hai điểm A, B có dạng: y = (b/a)x + b.