Bài 3: Đường thẳng song song và đường thẳng cắt nhau

C. HOẠT ĐỘNG LUYỆN TẬP

Câu 1: Trang 48 sách VNEN 9 tập 1

Đồ thị của hàm số y = $\frac{2}{5}$x - 7 cắt đồ thị hàm số nào dưới đây?

a) y = $\frac{2}{5}$x + 83 ;                            b) y = 0,4x + 3 ;

c) y = $\frac{4x - 1}{10}$ ;                           d) y = -$\frac{2}{5}$x + $\sqrt{3}$.

Câu 2: Trang 48 sách VNEN 9 tập 1

Hãy chỉ ra ba cặp đường thẳng cắt nhau và các cặp đường thẳng song song với nhau trong các đường thẳng sau:

y = 0,8x + 2;  y = 15 - 1,5x ;   y = -x + 6 ;   y = $\frac{4}{5}$x - 19 ; y = 1,5x - 15

Câu 3: Trang 48 sách VNEN 9 tập 1

Tìm tọa độ giao điểm của đồ thị các đồ thị hàm số:

a) y = 5x - 7 và y = 3x + 1 ;                                                              b) y = -3x + 2 và y = 8x - 9 ;

c) y = 0,4x - 5 và y = -0,1x - 3 ;                                                        d) y = 23x - 6 và y = -2x + 9 ;

e) y = 98x và y = -102x - 3 ;                                                              g) y = - 3 và y = 36x + 1.

Câu 4: Trang 48 sách VNEN 9 tập 1

Cho hàm số y = $\frac{1}{4}$x + 9. Viết công thức của các hàm số bậc nhất mà đồ thị của chúng:

a) Cắt đồ thị của hàm số đã cho

b) Song song với đồ thị của hàm số đã cho

Câu 5: Trang 48 sách VNEN 9 tập 1

Cho đường thẳng (d) y = ax + b. Tìm các giá trị của a, b trong mỗi trường hợp sau:

a) (d) song song với đường thẳng y = 3x + 5 ;

b) (d) trùng với đường thẳng y = -x + 2 ;

c) (d) cắt đường thẳng y = -$\sqrt{3}$x + 2 ;

d) (d) đi qua điểm A($\sqrt{3}$ - $\sqrt{2}$ ; 1 - $\sqrt{6}$) và B($\sqrt{2}$ ; 2).

Câu 6: Trang 49 sách VNEN 9 tập 1

Cho các đường thẳng 

(d1): y = x + 1 ;         (d2): y = -$\frac{1}{2}$x + 1 ;     (d3): y = -$\frac{1}{2}$x - 2.

a) Không vẽ đồ thị các hàm số đó, cho biết các đường thẳng có vị trí như thế nào với nhau.

b) Viết phương trình đường thẳng đi qua A(-2; 2) và song song với đường thẳng (d2).

D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG

Câu 1: Trang 49 sách VNEN 9 tập 1

Hãy tự kiểm chứng mệnh đề: Hai đường thẳng y = ax + b (a $\neq $ 0) và y = a'x + b' (a' $\neq $ 0) vuông góc với nhau khi và chỉ khi a.a' = 1

Vận dụng: Viết phương trình đường thẳng qua gốc tọa độ và vuông góc với đường thẳng (d1): y = x + 1.

Câu 2: Trang 49 sách VNEN 9 tập 1

Tính diện tích tam giác giới hạn bởi các đường  y = x; y = - x và y = 4.

Câu 3: Trang 49 sách VNEN 9 tập 1

Trên mặt phẳng tọa độ Oxy cho hai điểm A(1; 1) và C(-1 ; -1).

a) Tìm các điểm B và D sao cho tứ giác ABCD là hình vuông.

b) Viết phương trình các đường thẳng chứa cạnh của hình vuông

Câu 4: Trang 49 sách VNEN 9 tập 1

a) Viết phương trình các đường thẳng biết rằng các đường thẳng (d1), (d2), (d3) này theo thứ tự cắt trục tung tại các điểm có tung độ lần lượt là 1; $\sqrt{3}$ ; - $\sqrt{3}$ và tạo với trục Ox các góc $45^{\circ}$; $30^{\circ}$; $60^{\circ}$.

b) Cho đường thẳng (d'): y = ($\sqrt{m}$ - 1).x + 11. Tìm m để đường thẳng (d') song song với đường thẳng (d1).

c) Cho đường thẳng (d''): y = (2m - 1).x - 9. Tìm m để đường thẳng (d'') cắt cả hai đường thẳng (d1) và (d2).

Câu 5: Trang 49 sách VNEN 9 tập 1

Viết phương trình đường thẳng đi qua A(4; 0) cắt tia Oy tại B(0; b) và diện tích tam giác OAB bằng 12.

Câu 6: Trang 49 sách VNEN 9 tập 1

Trên mặt phẳng tọa độ Oxy cho ba điểm A(a; 0); B(0; b) (với a > 0, b > 0) và C(1; 2) như trên hình 12.

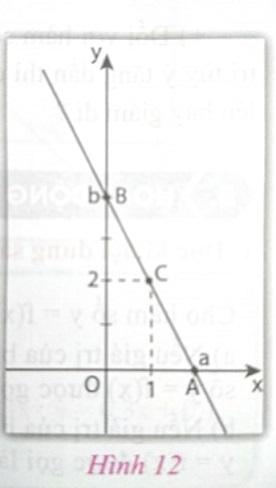
a) Viết phương trình đường thẳng đi qua hai điểm A, B

b) Tìm hệ thức liên hệ giữa a, b sao cho ba điểm A, B, C thẳng hàng.

c) Tìm các giá trị của a, b sai cho bao điểm A, B, C thẳng hàng và diện tích tam giác OAB nhỏ nhất.