Bài 8: Ôn tập chương I
Bài ôn tập chương I: Giải bài 8 trang 83
Trong bài học này, chúng ta sẽ cùng nhau giải đáp các câu hỏi và làm rõ kiến thức từ bài học. Bài 8 ôn tập chương I tập 1 trang 83 đưa ra một số vấn đề cần được giải quyết. Hãy theo dõi cách làm chi tiết và dễ hiểu dưới đây để nắm vững kiến thức.
Hy vọng rằng bài hướng dẫn này sẽ giúp các em học sinh hiểu rõ hơn về nội dung bài học và có khả năng áp dụng kiến thức vào thực tế. Hãy cùng nhau hoàn thiện kỹ năng và nắm vững kiến thức từ bài học để đạt được kết quả tốt nhất.
Bài tập và hướng dẫn giải
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 83 sách VNEN 9 tập 1
1. Điền vào chỗ chấm (...) để ôn tập các công thức đã học trong chương.
1.1. Các hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác ABC vuông tại A, đường cao AH (h.59)
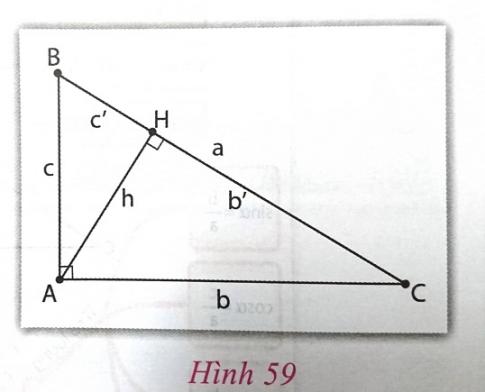
a) $b^{2}$ = ............ ; $c^{2}$ = ..................;
b) $h^{2}$ = .............;
c) b.c = .....................;
d) $\frac{1}{h^{2}}$ =..........................
1.2. Định nghĩa các tỉ số lượng giác của góc nhọn $\alpha $ (h.60)
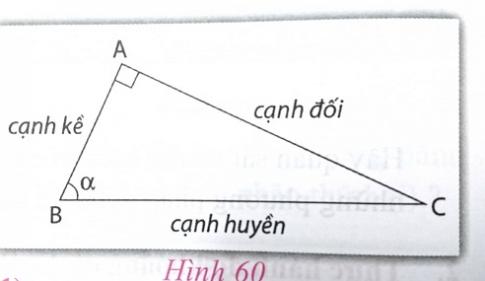
sin$\alpha $ = $\frac{....................}{....................}$ ; cos$\alpha $ = $\frac{....................}{....................}$ ;
tan$\alpha $ = $\frac{....................}{....................}$ ; cot$\alpha $ = $\frac{....................}{....................}$ .
1.3. Một số tính chất của các tỉ số lượng giác (h.61)

* Cho hai góc $\alpha $ phụ nhau. Khi đó
sin$\alpha $ =.......................; ................cot$\beta $ ;
cos$\alpha $ =......................; cot$\alpha $ =..............
* Cho góc nhọn $\alpha $. Ta có:
0 < sin$\alpha $ < 1 ; 0<........<1 ; $sin^{2}$$\alpha $ + $cos^{2}$$\alpha $ = ............ ;
tan$\alpha $ = $\frac{sin\alpha}{............}$ ; cot$\alpha $ = $\frac{...........}{............}$ ; tan$\alpha $.cot$\alpha $ = ................
1.4. Các hệ thức về cạnh và góc trong tam giác vuông
Cho tam giác ABC vuông tại A (h.62).
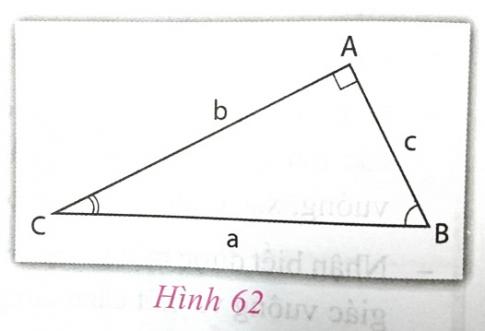
a) b = a.sin B = a.cos C ;
c = .............=..............
b) b = c.tan B =...............;
c = ............=................
Câu 3: Trang 85 sách VNEN 9 tập 1
Chọn đáp án đúng trong các câu sau
a) Cho $0^{\circ}$ < $\alpha $ < $90^{\circ}$. Khẳng định nào sau đây là đúng?
A. sin$\alpha $ + cos$\alpha $ = 1 B. tan$\alpha $ = tan ($90^{\circ}$ - $\alpha $)
C. sin$\alpha $ = cos($90^{\circ}$ - $\alpha $) D. cot$\alpha $ = cot($90^{\circ}$ -$\alpha $)
b) Cho tam giác ABC vuông tại A, đường cao AH. Biết AB = 6cm, BC = 7,5cm. Độ dài CH bằng:
A. 4,8cm B. 2,7cm C. 0,6cm D. $\frac{5}{3}$cm.
c) Cho tam giác ABC vuông tại A, $\widehat{B}$ = $\alpha $, AB =1cm, AC = 2cm. Khẳng định nào sau đây là sai?
A. sin$\alpha $ = 2cos$\alpha $ B.cot$\alpha $ = $\frac{1}{2}$
C. $\frac{sin\alpha - cos\alpha}{sin\alpha + cos\alpha}$ = $\frac{1}{3}$ D. $\frac{sin\alpha - 2cos\alpha}{sin\alpha + cos\alpha}$ = $\frac{1}{3}$.
Câu 4: Trang 85 sách VNEN 9 tập 1
Cho tam giác ABC có AB = 3,6cm, AC = 4,8cm, BC = 6cm.
a) Chứng minh tam giác ABC vuông tại A. Tính các góc B, C và đường cao AH của tam giác đó.
b) Gọi BD là phân giác của góc B. Tính tỉ số diện tích của tam giác ABD và tam giác BDC.
Câu 5: Trang 85 sách VNEN 9 tập 1
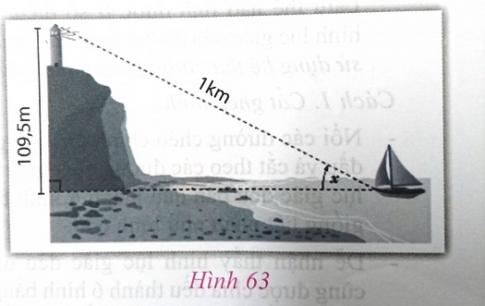
Ngọn hải đăng Long Châu tọa lạc trên đảo Long Châu, huyện đảo Cát Hải, Hải Phòng, cao 109,5m so với mực nước biển. Khoảng cách từ đỉnh của ngọn hải đăng đến một con thuyền đang neo trên biển là 1km. Một người đứng trên thuyền và nhìn lên ngọn hải đăng. Tính góc nhìn của người đó tạo với phương nằm ngang (h.63).
Câu 6: Trang 85 sách VNEN 9 tập 1
Cho tam giác ABC có góc B bằng $120^{\circ}$, BC =12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D
a) Tính độ dài đường phân giác BD
b) Gọi M là trung điểm của BC. Chứng minh AM $\perp $ BD.
c) Tính AM và diện tích tam giác ABM.
D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNG
Câu 1: Trang 86 sách VNEN 9 tập 1
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D và E lần lượt là hình chiếu của H trên AB, AC.
a) Cho BH = 4cm, CH = 9cm.
i) Tính độ dài đoạn thẳng DE và số đo góc HAC (làm tròn đến độ)
ii) Tính giá trị của biểu thức P = $\frac{2sinB + 3cosC}{tanB - 3cotC}$
iii) Các đường thẳng vuông góc với DE tại D và tại E lần lượt cắt BC tại M và N. Chứng minh M là trung điểm của BH và N là trung điểm của CH. Tính diện tích tứ giác DENM
b) Chứng minh AD.AB = AE.AC.
c) Qua A kẻ đường thẳng vuông góc với DE cắt BC tại I. Chứng minh I là trung điểm của BC.
d) Tam giác ABC có thêm điều kiện gì để diện tích tam giác ABC gấp đôi diện tích tứ giác ADHE.





