C. HOẠT ĐỘNG LUYỆN TẬPCâu 1: Trang 83 sách VNEN 9 tập 11. Điền vào chỗ chấm (...) để ôn tập các...
C. HOẠT ĐỘNG LUYỆN TẬP
Câu 1: Trang 83 sách VNEN 9 tập 1
1. Điền vào chỗ chấm (...) để ôn tập các công thức đã học trong chương.
1.1. Các hệ thức về cạnh và đường cao trong tam giác vuông
Cho tam giác ABC vuông tại A, đường cao AH (h.59)
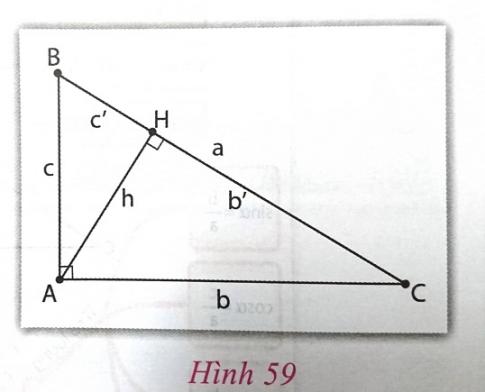
a) $b^{2}$ = ............ ; $c^{2}$ = ..................;
b) $h^{2}$ = .............;
c) b.c = .....................;
d) $\frac{1}{h^{2}}$ =..........................
1.2. Định nghĩa các tỉ số lượng giác của góc nhọn $\alpha $ (h.60)
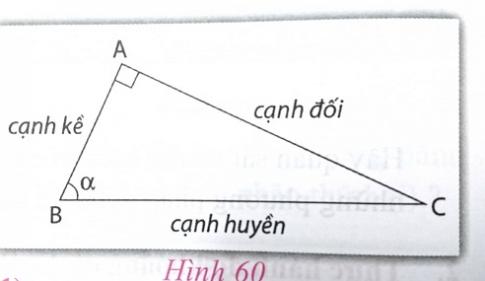
sin$\alpha $ = $\frac{....................}{....................}$ ; cos$\alpha $ = $\frac{....................}{....................}$ ;
tan$\alpha $ = $\frac{....................}{....................}$ ; cot$\alpha $ = $\frac{....................}{....................}$ .
1.3. Một số tính chất của các tỉ số lượng giác (h.61)

* Cho hai góc $\alpha $ phụ nhau. Khi đó
sin$\alpha $ =.......................; ................cot$\beta $ ;
cos$\alpha $ =......................; cot$\alpha $ =..............
* Cho góc nhọn $\alpha $. Ta có:
0 < sin$\alpha $ < 1 ; 0<........<1 ; $sin^{2}$$\alpha $ + $cos^{2}$$\alpha $ = ............ ;
tan$\alpha $ = $\frac{sin\alpha}{............}$ ; cot$\alpha $ = $\frac{...........}{............}$ ; tan$\alpha $.cot$\alpha $ = ................
1.4. Các hệ thức về cạnh và góc trong tam giác vuông
Cho tam giác ABC vuông tại A (h.62).
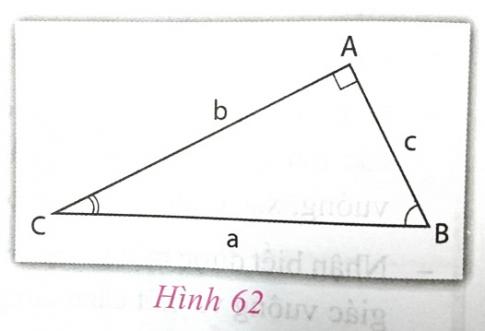
a) b = a.sin B = a.cos C ;
c = .............=..............
b) b = c.tan B =...............;
c = ............=................
- Câu 3: Trang 85 sách VNEN 9 tập 1Chọn đáp án đúng trong các câu saua) Cho$0^{\circ}$ <...
- Câu 4: Trang 85 sách VNEN 9 tập 1Cho tam giác ABC có AB = 3,6cm, AC = 4,8cm, BC = 6cm.a) Chứng minh...
- Câu 5: Trang 85 sách VNEN 9 tập 1Ngọn hải đăng Long Châu tọa lạc trên đảo Long Châu, huyện đảo Cát...
- Câu 6: Trang 85 sách VNEN 9 tập 1Cho tam giác ABC có góc B bằng$120^{\circ}$, BC =12cm, AB =...
- D.E. HOẠT ĐỘNG VẬN DỤNG và TÌM TÒI, MỞ RỘNGCâu 1: Trang 86 sách VNEN 9 tập 1Cho tam giác ABC vuông...






{ "content1": "1.1. a) $b^{2}$ = $c^{2} - h^{2}$ ; $c^{2}$ = $b^{2} + h^{2}$; b) $h^{2}$ = $a^{2} - H^{2}$; c) b.c = $a^{2}$; d) $\frac{1}{h^{2}}$ = $\frac{1}{a^{2}} + \frac{1}{b^{2}}$", "content2": "1.2. sin$\alpha $ = $\frac{BC}{AC}$ ; cos$\alpha $ = $\frac{AB}{AC}$ ; tan$\alpha $ = $\frac{BC}{AB}$ ; cot$\alpha $ = $\frac{AB}{BC}$", "content3": "1.3. * Cho hai góc $\alpha $ phụ nhau. Khi đó sin$\alpha $ = cos$\beta $ ; cos$\alpha $ = -sin$\alpha $ ; cot$\alpha $ = -tan$\alpha $ * Cho góc nhọn $\alpha $. Ta có: 0 < sin$\alpha $ < 1 ; 0 < cos$\alpha $ < 1 ; $sin^{2}$$\alpha $ + $cos^{2}$$\alpha $ = 1 ; tan$\alpha $ = $\frac{sin\alpha}{cos\alpha}$ ; cot$\alpha $ = $\frac{cos\alpha}{sin\alpha}$ ; tan$\alpha $.cot$\alpha $ = 1", "content4": "1.4. a) b = a.sin B = c.cos A ; c = a.cos B = b.sin A ; b) b = c.tan B = a.cos C ; c = b.cot B = a.sin C"}