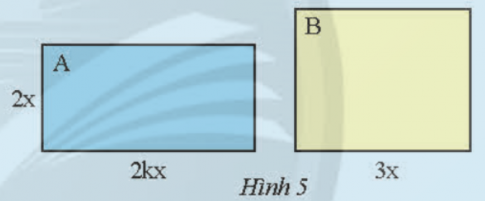
Khám phá 4 trang 15 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình chữ nhật A có chiều rộng...
Câu hỏi:
Khám phá 4 trang 15 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Hình chữ nhật A có chiều rộng 2x (cm), chiều dài gấp k (k > 1) lần chiều rộng. Hình chữ nhật B có chiều dài 3x (cm). Muốn hai hình chữ nhật này có diện tích bằng nhau thì B phải có chiều rộng bằng bao nhiêu?
Câu trả lời:
Người trả lời: GV. Đỗ Hồng Ánh
Phương pháp giải:Ta có diện tích hình chữ nhật A là S$_{A}$ = 4kx$^{2}$ (cm$^{2}$) và diện tích hình chữ nhật B là S$_{B}$ = R.3x (cm$^{2}$).Để hai hình chữ nhật này có diện tích bằng nhau, ta có phương trình:4kx$^{2}$ = R.3xGiải phương trình trên ta được:R = $\frac{4}{3}$ kx (cm)Vậy đáp án cho câu hỏi là: Để hai hình chữ nhật này có diện tích bằng nhau thì chiều rộng của hình chữ nhật B phải là $\frac{4}{3}$ kx (cm).
Câu hỏi liên quan:
- 1. Cộng, trừ hai đa thứcThực hành 1 trang 13 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Cho hai đa...
- 2. Nhân hai đa thứcThực hành 2 trang 14 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện các...
- Thực hành 3 trang 15 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Viết các biểu thức sau thành đa...
- Vận dụng 1 trang 15 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Viết biểu thức tính khoảng cách...
- Vận dụng 2 trang 13 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính diện tích phần tô màu trong...
- 3. Chia đa thức cho đơn thứcThực hành 4 trang 16 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực...
- Vận dụng 3 trang 15 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính diện tích đáy của hình hộp chữ...
- Thực hành 5 trang 16 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện các phép chia đa thức...
- Vận dụng 4 trang 13 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính chiều cao của hình hộp chữ...
- Bài tậpBài tập 1 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính:a) x + 2y + (x - y)b) 2x...
- Bài tập 2 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tìm độ dài cạnh còn thiếu của tam...
- Bài tập 3 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện phép nhân.a)...
- Bài tập 4 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện phép nhâna) (x - y)(x -...
- Bài tập 5 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện phép chia.a) $2...
- Bài tập 6 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Thực hiện phép chiaa)...
- Bài tập 7 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Tính giá trị của biểu thức:a)...
- Bài tập 8 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST: Trên một dòng sông, để đi được 10 km...
- Bài tập 9 trang 17 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Tính chiều dài của hình chữ...
- Khởi động trang 12 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Trên một đoạn sông thẳng, xuất...
- Khám phá 1 trang 12 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Tại một công trình xây dựng,...
- Khám phá 2 trang 13 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Hình hộp chữ nhật A có chiều...
- Khám phá 3 trang 14 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:a) Hình 3a là bản vẽ sơ lược sàn của...
- Khám phá 5 trang 16 sách giáo khoa (SGK) toán lớp 8 tập 1 CTST:Một bức tường được trang trí...






Vậy để hai hình chữ nhật A và B có diện tích bằng nhau, chiều rộng của hình chữ nhật B phải là 4x * k / 3 (cm).
Diện tích của hình chữ nhật B là chiều dài nhân chiều rộng, tức là 3x * b (cm^2). Để hai hình chữ nhật A và B có diện tích bằng nhau, ta có phương trình: 4x^2*k = 3x * b => b = 4x * k / 3 (cm).
Gọi chiều rộng của hình chữ nhật A là 2x (cm), chiều dài của hình chữ nhật A là 2x*k (cm) với k > 1. Diện tích của hình chữ nhật A là 2x * 2x*k = 4x^2*k (cm^2).