Hoạt động 3: Tính chất của kCna,Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo...
Câu hỏi:
Hoạt động 3: Tính chất của kCn
a,Quan sát ba dòng đầu, hoàn thành tiếp hai dòng cuối theo mẫu
(a + b)1 = a + b = C01a+C01bC10a+C10b
(a + b)2 = a2 + 2ab + b2 = C02a2+C12ab+C02b2C20a2+C21ab+C20b2
(a + b)3 = a3 + 3a2b + 3ab2 + b3 = C03a3+C13a2b+C23ab2+C03b3C30a3+C31a2b+C32ab2+C30b3
(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4 = ...
(a + b)5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5 = ...
Nhận xét rằng các hệ số khai triển của hai số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Hãy so sánh, chẳng hạn,![]() Từ đó hãy dự đoán hệ thức giữa
Từ đó hãy dự đoán hệ thức giữa ![]()
b) Dựa vào kết quả của HĐ3a, ta có thể viết những hàng đầu của tam giác Pascal dưới dạng:
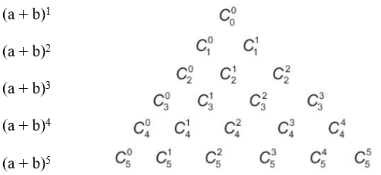
Từ tính chất của tam giác Pascal, hãy so sánh![]() Từ đó hãy dự đoán hệ thức giữa
Từ đó hãy dự đoán hệ thức giữa ![]()
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Linh
Phương pháp giải:Để giải câu hỏi trên, ta sử dụng khai triển bằng công thức nhị thức Newton.Công thức Newton:(a + b)^n = C0n*a^n + C1n*a^(n-1)*b + C2n*a^(n-2)*b^2 + ... + C(n-1)n*a*b^(n-1) + Cnn*b^nTrong đó, Ckn là hệ số nhân tử tổ hợp chập k của n (hay chính là số lượng k phần tử được chọn từ tập n phần tử).Câu trả lời:a) (a + b)^4 = a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4Dự đoán:Từ việc quan sát hệ số của khai triển (a + b)^4, ta thấy rằng hệ số của các số hạng cách đều số hạng đầu và số hạng cuối luôn bằng nhau. Như vậy, có thể dự đoán rằng hệ số tương ứng với các số hạng cách nhau i biệt đều bằng nhau sẽ là 4C4i. Vậy, chẳng hạn với (a + b)^5, hệ số của các số hạng cách nhau 1 biệt đều bằng nhau sẽ là 5C4*4 = 20 và ta có thể viết khai triển như sau:(a + b)^5 = a^5 + 5a^4b + 10a^3b^2 + 10a^2b^3 + 5ab^4 + b^5Dựa vào tính chất của tam giác Pascal, hệ thức giữa các biểu thức trên là C4a^4*a^(5-4-i)*b^i = C4*4a^(5-i)*b^i = 4C4i*a^(5-i)*b^i.
Câu hỏi liên quan:
- 1.TAM GIÁC PASCALHoạt động 1: Khai triển (a+b)^n, n thuộc {1;2;3;4;5}Trong Bài 25 sách giáo khoa...
- Hoạt động 2:Tam giác PascalViết các hệ số của khai triển (a + b)^nvới một số giá trị...
- Luyện tập 1:a, Sử dụng tam giác Pascal viết khai triển của (a+b)^7b, Sử dụng tam giá Pascal...
- 2. CÔNG THỨC NHỊ THỨC NEWTONLuyện tập 2: Khai triển (x-2y)^6
- Luyện tập 3: Tìm hệ số của X^7 trong khai triển đa thức của (2-3x)^10
- Vận dụng:a, Viết khai triển nhị thức Newton của (1+x)^nb, Cho x=1 trong khai triển ở câu a,...
- BÀI TẬP2.9. Sử dụng tam giá Pascal, viết khai triển:a, (x-1)^5b, (2x-3y)^4
- 2.10. Viết khai triển theo nhị thức Newtona, (x+y)^6b, (1-2y)^5
- 2.11.Tìm hệ số của x^8 trong khai triển của (2x-3)^10.
- 2.12. Biết hệ số của x^2 trong khai triển của (1-3x)^n là 90. Tìm n
- 2.13. Từ khai triển biểu thức (3x-5)^4 thành đa thức, hãy tính tổng các hệ số của đa thức nhận...
- 2.14. Tìm các hệ số của x^5 trong khai triển thành đa thức của biểu thứcx(1-2x)^5 +X^2(1+3x)^10.
- 2.15. Tính tổng sau đây
- 2.16. Tìm số tự nhiên n thỏa mãn
- 2.17.Tìm số nguyên dương n sao cho
- 2.18. Biết rằng (2+x)^100=a0+ a1x + a2x2+ ... + a100x^100. Với giá trị nào của k...
Bình luận (0)





