II. Hình chữ nhật cơ sởHoạt động 3.a) Quan sát điểm M (x; y) nằm trên hypebol (H) (Hình 15) và...
Câu hỏi:
II. Hình chữ nhật cơ sở
Hoạt động 3.
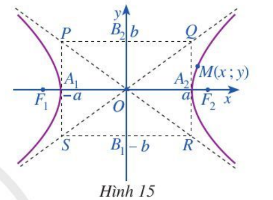
a) Quan sát điểm M (x; y) nằm trên hypebol (H) (Hình 15) và chứng tỏ rằng x ≤ –a hoặc x ≥ a.
b) Viết phương trình hai đường thẳng PR và QS.
Câu trả lời:
Người trả lời: GV. Đỗ Đăng Hưng
a) Phương pháp giải:- Ta biết rằng nếu điểm M(x; y) thuộc hypebol (H) thì $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$.- Vì $\frac{y^{2}}{b^{2}} \geq 0$ nên $\frac{x^{2}}{a^{2}}\geq 1 \Rightarrow x^{2} \geq a^{2} \Rightarrow x ≤ –a$ hoặc x ≥ a.b) Phương pháp giải:- Ta có điểm P(–a; b), R(a; –b), nên vectơ $\overrightarrow{PR}$ = (2a; -2b).- Chọn vectơ (b; a) là một vectơ pháp tuyến của PR, từ đó tìm được phương trình của đường thẳng PR: $y=-\frac{b}{a}x$.- Ta cũng có điểm Q(a; b), S(–a; –b), nên vectơ $\overrightarrow{QS}$ = (-2a; -2b).- Chọn vectơ (–b; a) là một vectơ pháp tuyến của QS, từ đó tìm được phương trình của đường thẳng QS: $y=\frac{b}{a}x$.Đáp án cho câu hỏi trên:a) Nếu điểm M thuộc hypebol (H) thì x ≤ –a hoặc x ≥ a.b) Phương trình đường thẳng PR là $y=-\frac{b}{a}x$ và phương trình đường thẳng QS là $y=\frac{b}{a}x$.
Câu hỏi liên quan:
- I. Tính đối xứng của HypebolHoạt động 1.Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có...
- Hoạt động 2.Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là...
- Luyện tập 1.Viết phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm...
- III. Tâm sai của HypebolHoạt động 4.Nêu định nghĩa tâm sai của elip có phương trình chính tắc...
- Luyện tập 2.Viết phương trình chính tắc của hypebol, biết độ dài trục ảo bằng 6 và tâm sai...
- IV. Bán kính qua tiêu cửa một điểm thuộc HypebolHoạt động 5.Trong mặt phẳng, xét đường...
- Hoạt động 6.Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức $MF1^{2}– MF2^{2}=...
- Luyện tập 3.Cho hypebol có phương trình chính tắc...
- V. Đường chuẩn của HypebolHoạt động 7.Cho hypebol (H) có phương trình chính tắc...
- Luyện tập 4.Tìm các tiêu điểm và đường chuẩn của hypebol có phương trình chính tắc là...
- VI. Cách vẽ đường HypebolHoạt động 8.Vẽ hypebol (H): $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$
- Luyện tập 5.Cho hypebol (H) có một đỉnh là A1(–4; 0) và tiêu cự là 10. Viết phương trình...
- Bài tậpBài tập 1.Viết phương trình chính tắc của hypebol, biết:a) Tiêu điểm là F1(– 3; 0) và...
- Bài tập 2.Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc...
- Bài tập 3.Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc là $x^{2}–...
- Bài tập 4.Trong mặt phẳng tọa độ Oxy, cho hypebol $(H): \frac{x^{2}}{64}-\frac{y^{2}}{36}=1$....
- Bài tập 5.Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để...
Bình luận (0)





