I. Tính đối xứng của HypebolHoạt động 1.Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có...
Câu hỏi:
I. Tính đối xứng của Hypebol
Hoạt động 1. Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, trong đó a > 0, b > 0 (Hình 13).
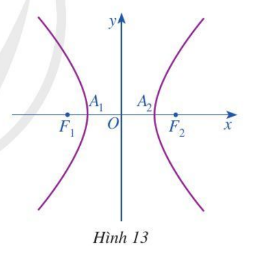
a) Tìm toạ độ hai tiêu điểm F1, F2 của hypebol (H).
b) Hypebol (H) cắt trục Ox tại các điểm A1, A2. Tìm độ dài các đoạn thẳng OA1 và OA2.
Câu trả lời:
Người trả lời: GV. Đỗ Thị Long
Phương pháp giải:a) Để tìm toạ độ hai tiêu điểm $F_{1}, F_{2}$ của hypebol (H), ta có phương trình: $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$So sánh với phương trình chuẩn của hypebol có dạng $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$, ta có:$a^{2}=c^{2}+b^{2}$Suy ra $c=\sqrt{a^{2}+b^{2}}$Do đó, $F_{1}(–c; 0)$ và $F_{2}(c; 0)$b) Ta có $A_{1}(x_{A1}; 0)$Thay toạ độ của $A_{1}$ vào phương trình chuẩn của hypebol ta được:$\frac{x_{A1}^{2}}{a^{2}}-\frac{0^{2}}{b^{2}}=1$$\Rightarrow x_{A1}^{2}=a^{2}$$\Rightarrow x_{A1} =a$ hoặc $x_{A1}=-a$Ta thấy $A_{1}$ nằm bên trái điểm O trên trục Ox nên $x_{A1}<0$Vậy $x_{A1}=-a$Nên $A_{1}(-a;0)$Khi đó $OA_{1}=\sqrt{(-a-0)^{2}+(0-0)^{2}} =\sqrt{(-a)^{2}}=a$Tương tự, ta có $A_{2}(x_{A2}; 0)$Suy ra $ x_{A2}^{2}=a^{2}$$x_{A2} =a$ hoặc $x_{A2}=-a$Ta thấy $A_{2}$ nằm bên phải điểm O trên trục Ox nên $x_{A2}>0$Vậy $x_{A2}=a$Nên $A_{2}(a;0)$Khi đó $OA_{2}=\sqrt{(a-0)^{2}+(0-0)^{2}} =\sqrt{a^{2}}=a$Vậy $OA_{1}=OA_{2}=a$.
Câu hỏi liên quan:
- Hoạt động 2.Trong mặt phẳng toạ độ Oxy, ta xét hypebol (H) có phương trình chính tắc là...
- II. Hình chữ nhật cơ sởHoạt động 3.a) Quan sát điểm M (x; y) nằm trên hypebol (H) (Hình 15) và...
- Luyện tập 1.Viết phương trình chính tắc của hypebol có một đỉnh là A2(5; 0) và một đường tiệm...
- III. Tâm sai của HypebolHoạt động 4.Nêu định nghĩa tâm sai của elip có phương trình chính tắc...
- Luyện tập 2.Viết phương trình chính tắc của hypebol, biết độ dài trục ảo bằng 6 và tâm sai...
- IV. Bán kính qua tiêu cửa một điểm thuộc HypebolHoạt động 5.Trong mặt phẳng, xét đường...
- Hoạt động 6.Với mỗi điểm M thuộc hypebol (H), từ hai đẳng thức $MF1^{2}– MF2^{2}=...
- Luyện tập 3.Cho hypebol có phương trình chính tắc...
- V. Đường chuẩn của HypebolHoạt động 7.Cho hypebol (H) có phương trình chính tắc...
- Luyện tập 4.Tìm các tiêu điểm và đường chuẩn của hypebol có phương trình chính tắc là...
- VI. Cách vẽ đường HypebolHoạt động 8.Vẽ hypebol (H): $\frac{x^{2}}{9}-\frac{y^{2}}{16}=1$
- Luyện tập 5.Cho hypebol (H) có một đỉnh là A1(–4; 0) và tiêu cự là 10. Viết phương trình...
- Bài tậpBài tập 1.Viết phương trình chính tắc của hypebol, biết:a) Tiêu điểm là F1(– 3; 0) và...
- Bài tập 2.Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc...
- Bài tập 3.Trong mặt phẳng toạ độ Oxy, cho hypebol có phương trình chính tắc là $x^{2}–...
- Bài tập 4.Trong mặt phẳng tọa độ Oxy, cho hypebol $(H): \frac{x^{2}}{64}-\frac{y^{2}}{36}=1$....
- Bài tập 5.Dọc theo bờ biển, người ta thiết lập hệ thống định vị vô tuyến dẫn đường tầm xa để...
Bình luận (0)





