Giải bài tập chuyên đề toán lớp 10 chân trời sáng tạo bài 2 nhị thức Newton

1. CÔNG THỨC NHỊ THỨC NEWTON

Hoạt động khám phá:  Có 3 hộp, mỗi hộp đựng hai quả cầu được dán nhãn a và b(H1)

Lấy từ mỗi hộp một quả cầu. Có bao nhiêu cách lấy để trong ba quả cầu lấy ra:

a) có 3 quả cầu dán nhãn b?

b) có 2 quả cầu dán nhãn b?

c) có 1 quả cầu dán nhãn b?

d) không có quả cầu nào dán nhãn b?

Thực hành 1: Hãy khai triển

a, $(a-b))^{6}$

b, $(1+x)^{7}$

2. TAM GIÁ PASCAL

Hoạt động khám phá 2: Từ các công thức khai triển:

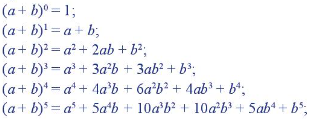
 có thể dự đoán rằng, với mỗi n∈N∗n∈ℕ*,

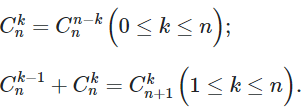
 Hãy chứng minh các công thức trên.

Thực hành 2: Sử dụng tam giác Pascal, hãy khai triển:

a) $(2x+1)^{6}$

b) $(2x+1)^{6}$

3.VẬN DỤNG CÔNG THỨC NHỊ THỨC NEWTON

Thực hành 3: Xác định hệ số của $x^{2}$ trong khai triển 

$(3x+2)^{9}$

Thực hành 4: Biết rằng trong khai triển của $(x+a)^6$ với a là một số thực, hệ số của 

x4">$x^4$ là 60. Tìm giá trị của a.

Thực hành 5: Chứng minh với mọi

n∈N∗, ta có

Vận dụng: Trong hộp A có 10 quả cầu được đánh số từ 1 đến 10. Người ta lấy một số quả cầu từ hộp A rồi cho vào hộp B. Có tất cả bao nhiêu cách lấy, tính cả trường hợp lấy 0 quả (tức là không lấy quả nào)?

BÀI TẬP

1. Khai triển biểu thức

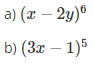
2. Tìm hệ số của 

$x^{10}$ trong khai triển của biểu thức $(2-x)^{12}$

3. Biết rằng a là một số thực khác 0 và trong khai triển của $(ax + 1)^6$, hệ số của x4 gấp bốn lần hệ số của $x^2$. Tìm giá trị của a.

4. Biết rằng hệ số của $x^2$ trong khai triển của $(1+3x)^n$ là 90. Tìm giá trị của n

5. Chứng minh công thức nhị thức Newton ( công thức(1) trang 35) bằng phương pháp quy nạp toán học

6. Biết rằng $(3x-1)^7$ = a0 + a1x + $a2x^2$2+ $a3x^3$ + $a4x^4$ + $a5x^5$ + $a6x^6$ + $a7x^7$.

a) a0 + a1 + a2 + a3 + a4 + a5 + a6 + a7;

b) a0 + a2 + a4 + a6.

7. Một tập hợp có 12 phần tử thì có tất cả bao nhiêu tập hợp con?

8. Từ 15 bút chì màu có màu khác nhau đôi một,

a) Có bao nhiêu cách chọn ra một số bút chì màu, tính cả trường hợp không chọn cái nào?

b) Có bao nhiêu cách chọn ra ít nhất 8 bút chì màu?